Giải bài 7.26 trang 35 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.26 trang 35 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 7.26 trang 35 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học tập tốt hơn.
Một viên bi được thả lăn trên một mặt phẳng nằm nghiêng (so với mặt phẳng nằm ngang).
Đề bài
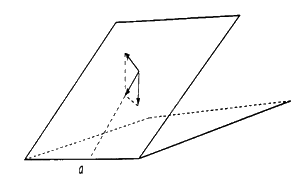
Một viên bi được thả lăn trên một mặt phẳng nằm nghiêng (so với mặt phẳng nằm ngang). Coi viên bi chịu tác dụng của hai lực chính là lực hút của Trái Đất (theo phương thẳng đứng, hướng xuống dưới) và phản lực, vuông góc với mặt phẳng nằm nghiêng, hướng lên trên. Giải thích vì sao viên bi di chuyển trên một đường thẳng vuông góc với giao tuyến của mặt phẳng nằm nghiêng và mặt phẳng nằm ngang.
Phương pháp giải - Xem chi tiết
Biểu diễn các lực tác dụng lên viên bi gồm trọng lực và phản lực
Tổng hợp lực của trọng lực và phản lực theo phương pháp tìm tổng hai vecto chung gốc bằng cách dựng hình bình hành
Lời giải chi tiết
Gọi a là giao tuyến của mặt phẳng nằm ngang và mặt phẳng nằm nghiêng. Phương của lực hút trái đất vuông góc với mặt phẳng nằm ngang, phương của phản lực vuông góc với mặt phẳng nghiêng nên phương của hai lực nói trên đều vuông góc với đường thẳng \({\rm{a}}\), do đó đường thẳng a vuông góc với mặt phẳng \(\left( P \right)\) chứa hai phương của hai lực đó.
Vì tổng hợp lực của trọng lực và phản lực là một lực có phương nằm trên mặt phẳng \(\left( P \right)\) nên phương đó vuông góc với \({\rm{a}}\). Do đó, viên bi lăn dọc theo đường thẳng vuông góc với đường thẳng \({\rm{a}}\).
Giải bài 7.26 trang 35 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp
Bài 7.26 trang 35 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế, hoặc chứng minh các đẳng thức liên quan đến đạo hàm.
Nội dung bài tập 7.26
Bài 7.26 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số tại một điểm cho trước.
- Tìm đạo hàm của hàm số.
- Vận dụng đạo hàm để giải các bài toán về cực trị, khoảng đơn điệu của hàm số.
- Ứng dụng đạo hàm để giải các bài toán thực tế liên quan đến tốc độ thay đổi.
Phương pháp giải bài tập 7.26
Để giải quyết bài tập 7.26 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Các công thức đạo hàm cơ bản: Đạo hàm của các hàm số đơn giản như xn, sinx, cosx, tanx, ex, ln(x).
- Các quy tắc đạo hàm: Quy tắc cộng, trừ, nhân, chia, quy tắc hàm hợp.
- Ứng dụng của đạo hàm: Tìm cực trị, khoảng đơn điệu, giải các bài toán thực tế.
Lời giải chi tiết bài 7.26 trang 35 SBT Toán 11 - Kết nối tri thức
(Ở đây sẽ là lời giải chi tiết của bài tập 7.26. Ví dụ:)
Bài 7.26: Cho hàm số f(x) = x3 - 3x2 + 2. Tìm đạo hàm f'(x) và xác định các điểm cực trị của hàm số.
Giải:
f'(x) = 3x2 - 6x
Để tìm điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy x = 0 hoặc x = 2.
Ta xét dấu f'(x) trên các khoảng:
- Khi x < 0, f'(x) > 0, hàm số đồng biến.
- Khi 0 < x < 2, f'(x) < 0, hàm số nghịch biến.
- Khi x > 2, f'(x) > 0, hàm số đồng biến.
Vậy hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2 và đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Luyện tập thêm
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 11 Kết nối tri thức và các tài liệu tham khảo khác.
Bảng tổng hợp các công thức đạo hàm thường dùng
| Hàm số | Đạo hàm |
|---|---|
| y = xn | y' = nxn-1 |
| y = sinx | y' = cosx |
| y = cosx | y' = -sinx |
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về cách giải bài tập 7.26 trang 35 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!