Giải bài 7.8 trang 28 SBT Toán 11 Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 7.8 trang 28 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học tập tốt hơn.
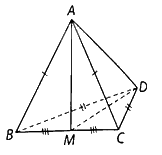
Cho tứ diện \(ABCD\) có \(AB = AC\) và \(DB = DC\). Chứng minh rằng \(AD \bot BC\).
Giải bài 7.8 trang 28 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp
Bài 7.8 trang 28 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế, hoặc chứng minh các đẳng thức liên quan đến đạo hàm. Để giải quyết bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm cơ bản về đạo hàm, các quy tắc tính đạo hàm và các ứng dụng của đạo hàm.
Nội dung chi tiết bài 7.8 trang 28 SBT Toán 11 Kết nối tri thức
Bài 7.8 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của một hàm số cho trước. Các em cần áp dụng các quy tắc tính đạo hàm đã học để tìm ra đạo hàm của hàm số.
- Dạng 2: Tìm đạo hàm cấp hai: Yêu cầu tìm đạo hàm cấp hai của một hàm số. Các em cần tính đạo hàm cấp một trước, sau đó tính đạo hàm của đạo hàm cấp một để tìm ra đạo hàm cấp hai.
- Dạng 3: Ứng dụng đạo hàm để giải quyết bài toán thực tế: Yêu cầu sử dụng đạo hàm để giải quyết các bài toán liên quan đến vận tốc, gia tốc, hoặc các bài toán tối ưu hóa.
Lời giải chi tiết bài 7.8 trang 28 SBT Toán 11 Kết nối tri thức
Dưới đây là lời giải chi tiết cho từng phần của bài 7.8 trang 28 sách bài tập Toán 11 Kết nối tri thức:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1
Lời giải:
f'(x) = 3x2 + 4x - 5
Ví dụ 2: Tìm đạo hàm cấp hai của hàm số g(x) = sin(x) + cos(x)
Lời giải:
g'(x) = cos(x) - sin(x)
g''(x) = -sin(x) - cos(x)
Ví dụ 3: Một vật chuyển động với vận tốc v(t) = 3t2 - 6t + 2 (m/s). Tính gia tốc của vật tại thời điểm t = 2s.
Lời giải:
Gia tốc a(t) là đạo hàm của vận tốc v(t).
a(t) = v'(t) = 6t - 6
a(2) = 6(2) - 6 = 6 (m/s2)
Mẹo giải bài tập đạo hàm hiệu quả
Để giải bài tập đạo hàm một cách hiệu quả, các em nên:
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm tính đạo hàm.
- Kiểm tra lại kết quả sau khi giải xong.
Tài liệu tham khảo thêm
Các em có thể tham khảo thêm các tài liệu sau để hiểu rõ hơn về đạo hàm:
- Sách giáo khoa Toán 11
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến
Kết luận
Hy vọng bài giải chi tiết bài 7.8 trang 28 sách bài tập Toán 11 Kết nối tri thức này sẽ giúp các em hiểu rõ hơn về đạo hàm và giải quyết các bài tập liên quan một cách hiệu quả. Chúc các em học tập tốt!
