Giải bài 7.3 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.3 trang 26 SBT Toán 11 - Kết nối tri thức
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 7.3 trang 26 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ giúp học sinh nắm vững kiến thức, phương pháp giải và tự tin làm bài tập Toán 11.
Chúng tôi luôn cập nhật đáp án nhanh chóng và chính xác nhất, hỗ trợ tối đa cho quá trình học tập của bạn.
Cho tứ diện \(ABCD\), gọi \(M\) và \(N\) lần lượt là trung điểm của \(AC\) và \(BD\).
Đề bài
Cho tứ diện \(ABCD\), gọi \(M\) và \(N\) lần lượt là trung điểm của \(AC\) và \(BD\). Biết \(MN = a\sqrt 3 ;AB = 2\sqrt 2 a\) và \(CD = 2a\). Chứng minh rằng đường thẳng \(AB\) vuông góc với đường thẳng \(CD\).
Phương pháp giải - Xem chi tiết
Chứng minh góc giữa đường thẳng \(AB\) và \(CD\) bằng \({90^ \circ }\)
+ Bước 1: Tính góc giữa hai đường thẳng \(AB\) và \(CD\) bằng \({90^ \circ }\)
+ Bước 2: Kết luận đường thẳng \(AB\) vuông góc với đường thẳng \(CD\).
Chú ý sử dụng định lý đảo Pytago để chứng minh tam giác là tam giác vuông
Lời giải chi tiết
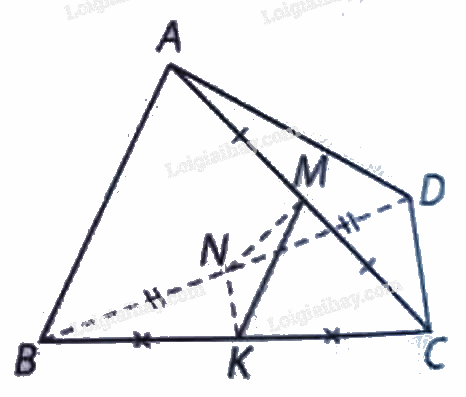
Lấy \(K\) là trung điểm của cạnh \(BC\), ta có: \(NK\) và \(MK\) lần lượt là đường trung bình của tam giác \(BCD\) và tam giác \(ABC\) nên \(NK = a,MK = a\sqrt 2 \).
Do đó, \(M{N^2} = 3{a^2} = N{K^2} + M{K^2}\) suy ra tam giác \(MNK\) vuông tại \(K\), hay \(MK \bot NK\), mà \(MK//AB\) và \(NK//CD\) nên \(\left( {AB,CD} \right) = \left( {MK,NK} \right) = {90^ \circ }\), hay \(AB \bot CD\).
Giải bài 7.3 trang 26 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 7.3 trang 26 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về phép biến hình. Bài tập này tập trung vào việc vận dụng các kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán hình học cụ thể. Việc nắm vững các tính chất và công thức liên quan đến các phép biến hình là chìa khóa để giải quyết thành công bài tập này.
Nội dung chi tiết bài 7.3 trang 26 SBT Toán 11
Bài 7.3 thường bao gồm các dạng bài tập sau:
- Dạng 1: Xác định ảnh của điểm, đường thẳng, hình qua phép biến hình. Yêu cầu học sinh xác định vị trí mới của các đối tượng hình học sau khi thực hiện một hoặc nhiều phép biến hình.
- Dạng 2: Tìm tâm, trục, góc của phép biến hình. Yêu cầu học sinh xác định các yếu tố quan trọng của phép biến hình dựa trên thông tin về ảnh và điểm gốc.
- Dạng 3: Chứng minh tính chất hình học sử dụng phép biến hình. Yêu cầu học sinh sử dụng các phép biến hình để chứng minh các tính chất liên quan đến sự bằng nhau, song song, vuông góc của các hình.
Lời giải chi tiết bài 7.3 trang 26 SBT Toán 11 - Kết nối tri thức
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 7.3 trang 26, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi:
Câu a)
(Giả sử đề bài là: Cho điểm A(1;2). Tìm ảnh A' của A qua phép tịnh tiến theo vectơ v = (3;-1))
Lời giải:
Áp dụng công thức phép tịnh tiến: A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)
Thay số: A'(1 + 3; 2 - 1) = A'(4; 1)
Vậy ảnh A' của A qua phép tịnh tiến theo vectơ v là A'(4; 1).
Câu b)
(Giả sử đề bài là: Cho đường thẳng d: x + y - 2 = 0. Tìm ảnh d' của d qua phép quay tâm O, góc 90 độ)
Lời giải:
Để tìm ảnh của đường thẳng d qua phép quay, ta cần tìm hai điểm thuộc d và tìm ảnh của chúng qua phép quay. Sau đó, vẽ đường thẳng đi qua hai điểm ảnh này, đó chính là d'.
(Tiếp tục trình bày chi tiết lời giải cho câu b và các câu còn lại, nếu có)
Mẹo giải bài tập phép biến hình
- Nắm vững định nghĩa và tính chất của từng phép biến hình.
- Sử dụng công thức biến đổi tọa độ một cách chính xác.
- Vẽ hình minh họa để dễ dàng hình dung và tìm ra hướng giải quyết.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tusach.vn - Đồng hành cùng bạn học Toán 11
Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập môn Toán 11. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các mẹo giải bài tập hữu ích. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!