Giải bài 4.13 trang 59 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.13 trang 59 SBT Toán 11 Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 4.13 trang 59 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học tập tốt hơn.
Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD.
Đề bài
Cho tứ diện ABCD. Gọi M, N, P lần lượt là các điểm thuộc các cạnh AB, BC, CD. Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP) trong các trường hợp sau:
a, Đường thẳng NP song song với đường thẳng BD.
b, Đường thẳng NP cắt BD.
Phương pháp giải - Xem chi tiết
Dựa vào định lý về 3 đường giao tuyến của 3 mặt phẳng: Nếu có 2 giao tuyến của song song với nhau thì giao tuyến thứ 3 cũng song song với 2 giao tuyến đó. Còn nếu có 2 giao tuyến cắt nhau thì 3 giao tuyến đó đồng quy.
Lời giải chi tiết
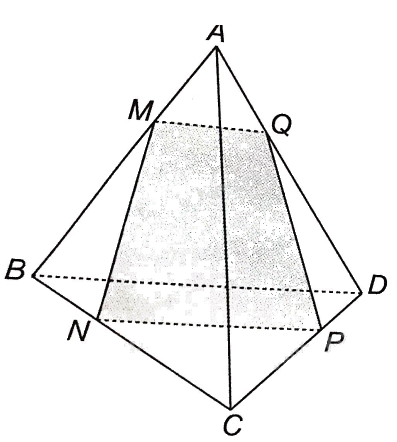
a,
NP là giao tuyến của hai mặt phẳng (MNP và (BCD
BD là giao tuyến của hai mặt phẳng (ABD và (BCD
Mà NP // BD nên giao tuyến của (MNP và (ABD cũng là một đường thẳng song song với NP và BD.
Ta thấy M thuộc AB nên M là điểm chung của (MNP và (ABD.
Vậy giao tuyến của (MNP và (ABD là đường thẳng d đi qua M, song song với NP và BD.
Trong mặt phẳng (ABD, gọi Q là giao điểm giữa d và AD.
Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP chính là điểm Q.
b,
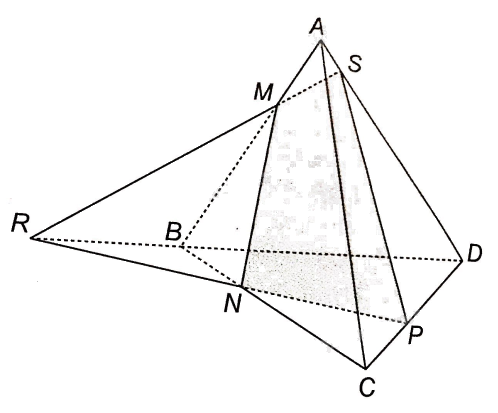
NP là giao tuyến của hai mặt phẳng (MNP) và (BCD)
BD là giao tuyến của hai mặt phẳng (ABD) và (BCD)
Mà đường thẳng NP và BD cắt nhau nên giao tuyến d của (MNP) và (ABD) là một đường thẳng đồng quy với NP và BD. (gọi R là giao điểm của NP và BD, vậy d đi qua điểm R
Ta thấy M thuộc AB nên M là điểm chung của (MNP) và (ABD). Vậy M thuộc đường giao tuyến d.
Trong mặt phẳng (BCD) gọi S là giao điểm của MR và BD, vậy giao tuyến d cũng sẽ đi qua điểm S.
Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) chính là điểm S.
Giải bài 4.13 trang 59 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp
Bài 4.13 trang 59 sách bài tập Toán 11 Kết nối tri thức là một bài tập thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức liên quan đến đạo hàm, đồng thời rèn luyện kỹ năng giải toán và tư duy logic.
Nội dung bài tập 4.13 trang 59 SBT Toán 11 Kết nối tri thức
Bài tập 4.13 thường xoay quanh việc tính đạo hàm của các hàm số phức tạp, hoặc ứng dụng đạo hàm để tìm cực trị, khoảng đơn điệu của hàm số. Cụ thể, bài tập có thể yêu cầu:
- Tính đạo hàm của hàm số y = f(x) tại một điểm x0.
- Tìm đạo hàm của hàm số y = f(x) trên một khoảng xác định.
- Xác định các điểm cực trị của hàm số y = f(x).
- Tìm khoảng đồng biến, nghịch biến của hàm số y = f(x).
Lời giải chi tiết bài 4.13 trang 59 SBT Toán 11 Kết nối tri thức
Để giúp các em hiểu rõ hơn về cách giải bài tập này, Tusach.vn xin trình bày lời giải chi tiết như sau:
(Giả sử bài tập cụ thể là: Tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1)
Lời giải:
Để tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1, ta sử dụng các quy tắc đạo hàm cơ bản:
- Đạo hàm của xn là nxn-1.
- Đạo hàm của một hằng số là 0.
- Đạo hàm của một tổng (hoặc hiệu) là tổng (hoặc hiệu) các đạo hàm.
Áp dụng các quy tắc trên, ta có:
f'(x) = 3x2 - 6x + 2
Các dạng bài tập tương tự và phương pháp giải
Ngoài bài tập 4.13, các em có thể gặp các bài tập tương tự về đạo hàm. Để giải quyết các bài tập này, các em cần:
- Nắm vững các quy tắc đạo hàm cơ bản.
- Rèn luyện kỹ năng biến đổi đại số.
- Phân tích bài toán và lựa chọn phương pháp giải phù hợp.
Lưu ý khi giải bài tập về đạo hàm
Khi giải bài tập về đạo hàm, các em cần lưu ý một số điểm sau:
- Kiểm tra kỹ điều kiện xác định của hàm số.
- Sử dụng đúng các quy tắc đạo hàm.
- Biết cách biến đổi đại số để đơn giản hóa biểu thức.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Đồng hành cùng các em trên con đường học tập
Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và phương pháp giải bài tập hiệu quả. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất!
| Chương | Bài | Nội dung |
|---|---|---|
| 4 | 4.13 | Giải bài tập về đạo hàm |
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài tập 4.13 trang 59 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!