Giải bài 4.42 trang 71 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.42 trang 71 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Bài viết này của tusach.vn sẽ cung cấp lời giải chi tiết và dễ hiểu bài 4.42 trang 71 sách bài tập Toán 11 Kết nối tri thức. Chúng tôi sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Hãy cùng tusach.vn khám phá lời giải chi tiết ngay sau đây!
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Gọi O là giao điểm của AC và BD.
Đề bài
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Gọi O là giao điểm của AC và BD. Gọi O’ là hình chiếu của O qua phép chiếu song song lên mặt phẳng (A’B’C’D’) theo phương AA’. Chứng minh rằng O’ là giao điểm của A’C’ và B’D’.
Phương pháp giải - Xem chi tiết
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Lời giải chi tiết
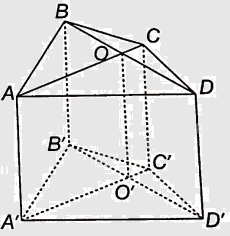
Qua phép chiếu lên mặt phẳng (A’B’C’D’) theo phương AA’, các điểm A, B, C, D, O lần lượt có hình chiếu là A’, B’, C’, D’, O’. Vì phép chiếu song song bảo toàn tính thẳng hàng của các điểm và O nằm giữa A và C nên O’ nằm giữa A’ và C’; Vì phép chiếu song song bảo toàn tính thẳng hàng của các điểm và O nằm giữa B và D nên O’ nằm giữa B’ và D’. Vậy O’ là giao điểm của A’C’ và B’D’.
Giải bài 4.42 trang 71 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp
Bài 4.42 trang 71 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng, và các tính chất liên quan để giải quyết các bài toán về vị trí tương đối giữa đường thẳng và mặt phẳng, hoặc tính khoảng cách.
Nội dung bài 4.42 trang 71 SBT Toán 11 - Kết nối tri thức
Bài 4.42 thường bao gồm các dạng bài tập sau:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng (song song, cắt nhau, nằm trong mặt phẳng).
- Tính góc giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ một điểm đến mặt phẳng, hoặc từ đường thẳng đến mặt phẳng.
- Tìm giao điểm của đường thẳng và mặt phẳng.
Lời giải chi tiết bài 4.42 trang 71 SBT Toán 11 - Kết nối tri thức
Để giải bài 4.42 trang 71 SBT Toán 11 Kết nối tri thức một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Vectơ chỉ phương của đường thẳng: Vectơ này cho biết hướng của đường thẳng.
- Vectơ pháp tuyến của mặt phẳng: Vectơ này vuông góc với mọi vectơ nằm trong mặt phẳng.
- Phương trình đường thẳng: Có nhiều dạng phương trình đường thẳng, tùy thuộc vào thông tin đã cho (điểm đi qua và vectơ chỉ phương, hai điểm đi qua,...).
- Phương trình mặt phẳng: Phương trình mặt phẳng có dạng Ax + By + Cz + D = 0, trong đó (A, B, C) là vectơ pháp tuyến của mặt phẳng.
Ví dụ minh họa (giả định bài toán cụ thể):
Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Chứng minh rằng đường thẳng d song song với mặt phẳng (P).
Lời giải:
Vectơ chỉ phương của đường thẳng d là a = (1, -1, 2). Vectơ pháp tuyến của mặt phẳng (P) là n = (2, -1, 1). Ta có:
a.n = (1)(2) + (-1)(-1) + (2)(1) = 2 + 1 + 2 = 5 ≠ 0
Vì tích vô hướng của vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng khác 0, nên đường thẳng d không song song với mặt phẳng (P). (Đây chỉ là ví dụ, cần giải bài toán cụ thể để có kết quả chính xác)
Mẹo giải bài tập Toán 11 - Kết nối tri thức
- Vẽ hình: Vẽ hình minh họa giúp các em hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Sử dụng công thức: Nắm vững các công thức liên quan đến vectơ, phương trình đường thẳng, phương trình mặt phẳng.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn - Đồng hành cùng các em học Toán 11
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập môn Toán 11. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách giáo khoa và sách bài tập Toán 11 Kết nối tri thức. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất!
| Chương | Bài | Liên kết |
|---|---|---|
| 1 | 1.1 | Giải bài 1.1 trang 5 |
| 2 | 2.2 | Giải bài 2.2 trang 20 |