Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 7.34 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
SBT Toán 11 - Kết nối tri thức
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Chương VII. Quan hệ vuông góc trong không gian
Bài 27. Thể tích

Giải bài 7.34 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.34 trang 41 SBT Toán 11 - Kết nối tri thức

Chào các em học sinh! Tusach.vn xin giới thiệu đến các em lời giải chi tiết bài 7.34 trang 41 sách bài tập Toán 11 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.

Chúng tôi hy vọng với lời giải này, các em sẽ hiểu rõ hơn về phương pháp giải và tự tin hơn khi làm bài tập.

Cho khối chóp đều (S.ABCD) có đáy (ABCD) là hình vuông cạnh bằng (a)

Đề bài

Cho khối chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), góc giữa mặt phẳng \(\left( {SCD} \right)\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(60^\circ \). Tính theo \(a\) thể tích khối chóp \(S.ABCD\).

Phương pháp giải - Xem chi tiếtGiải bài 7.34 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Áp dụng công thức tính thể tích khối chóp: \(S = \frac{1}{3}Bh\).

Trong đó: \(B\) là diện tích đa giác đáy

\(h\)là đường cao của hình chóp

Bước 1: Xác định chiều cao \(SO\)

Bước 2: Tính diện tích đáy

Bước 3: Tính thể tích khối chóp \(V = \frac{1}{3}SO.{S_{ABCD}}\).

Lời giải chi tiết

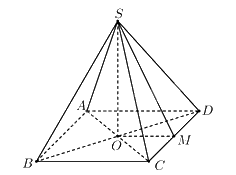
Giải bài 7.34 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

Gọi \(O\) là giao điểm của \(AC\) và \(BD\), ta có \(SO\) vuông góc với mặt đáy \(\left( {ABCD} \right)\). Kẻ \(OM\) vuông góc với \(CD\) tại \(M\) thì \(SM\) cũng vuông góc với \(CD\) nên góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng góc giữa hai đường thẳng \(SM\) và \(OM\), mà \(\left( {SM,OM} \right) = \widehat {SMO} = 60^\circ \). Ta có: \(OM = \frac{a}{2};\)\(SO = OM \cdot {\rm{tan}}\widehat {SMO} = \frac{{a\sqrt 3 }}{2}\). Vậy \({V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{1}{3} \cdot {a^2} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{{6}}\).

Giải bài 7.34 trang 41 SBT Toán 11 - Kết nối tri thức: Hướng dẫn chi tiết

Bài 7.34 trang 41 sách bài tập Toán 11 Kết nối tri thức yêu cầu chúng ta tìm cực trị của hàm số. Để giải bài này, chúng ta cần nắm vững kiến thức về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, cũng như các bước kiểm tra điều kiện đó.

Đề bài:

Tìm các điểm cực trị của hàm số sau:

  • a) f(x) = x3 - 3x2 + 2
  • b) f(x) = -x4 + 4x2

Lời giải:

a) f(x) = x3 - 3x2 + 2
  1. Tính đạo hàm cấp nhất: f'(x) = 3x2 - 6x
  2. Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được: 3x2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2
  3. Tính đạo hàm cấp hai: f''(x) = 6x - 6
  4. Kiểm tra điều kiện cực trị:
    • f''(0) = -6 < 0 => Hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 2
    • f''(2) = 6 > 0 => Hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = 8 - 12 + 2 = -2
  5. Kết luận: Hàm số đạt cực đại tại x = 0, f(0) = 2 và đạt cực tiểu tại x = 2, f(2) = -2
b) f(x) = -x4 + 4x2
  1. Tính đạo hàm cấp nhất: f'(x) = -4x3 + 8x
  2. Tìm điểm dừng: Giải phương trình f'(x) = 0, ta được: -4x3 + 8x = 0 => -4x(x2 - 2) = 0 => x = 0 hoặc x = ±√2
  3. Tính đạo hàm cấp hai: f''(x) = -12x2 + 8
  4. Kiểm tra điều kiện cực trị:
    • f''(0) = 8 > 0 => Hàm số đạt cực tiểu tại x = 0. Giá trị cực tiểu là f(0) = 0
    • f''(√2) = -12(2) + 8 = -16 < 0 => Hàm số đạt cực đại tại x = √2. Giá trị cực đại là f(√2) = -4 + 8 = 4
    • f''(-√2) = -12(2) + 8 = -16 < 0 => Hàm số đạt cực đại tại x = -√2. Giá trị cực đại là f(-√2) = -4 + 8 = 4
  5. Kết luận: Hàm số đạt cực tiểu tại x = 0, f(0) = 0 và đạt cực đại tại x = √2 và x = -√2, f(√2) = f(-√2) = 4

Lưu ý khi giải bài tập cực trị:

  • Luôn kiểm tra điều kiện cần và đủ để hàm số đạt cực trị.
  • Chú ý đến tập xác định của hàm số.
  • Sử dụng đạo hàm cấp hai để xác định loại cực trị (cực đại hay cực tiểu).

Hy vọng bài giải này sẽ giúp các em hiểu rõ hơn về cách giải bài tập cực trị của hàm số. Chúc các em học tốt!

Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN