Giải bài 7.40 trang 41 SBT Toán 11 - Kết nối tri thức

Giải bài 7.40 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.40 trang 41 SBT Toán 11 Kết nối tri thức

Bài 7.40 trang 41 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của các bạn.

Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh \(1{\rm{\;m}}\)

Đề bài

Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh \(1{\rm{\;m}}\) để gò lại thành một chiếc thùng có dạng hình hộp chữ nhật không nắp. Hỏi cạnh của các hình vuông cần bỏ đi có độ dài bằng bao nhiêu để thùng hình hộp nhận được có thể tích lớn nhất?

Phương pháp giải - Xem chi tiết Giải bài 7.40 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Áp dụng công thức tính thể tích khối hộp chữ nhật: \({\rm{V}} = a.b.c\).

Trong đó: \(a,b,c\) là độ dài 3 cạnh hình hộp chữ nhật có chung 1 đỉnh

Bước 1: Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0 < x < \frac{1}{2}\) ).

Tính thể tích hình hộp chữ nhật nhận được

Bước 2: Tìm giá trị lớn nhất của thể tích hình hộp chữ nhật nhận được

Từ đó tìm \(x\)

Lời giải chi tiết

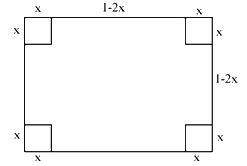
Giải bài 7.40 trang 41 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

Gọi \(x\left( {{\rm{\;m}}} \right)\) là chiều dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với \(0 < x < \frac{1}{2}\) ).

Thể tích hình hộp chữ nhật nhận được là

\(V = {(1 - 2x)^2} \cdot x = \frac{1}{4} \cdot \left( {1 - 2x} \right) \cdot \left( {1 - 2x} \right) \cdot 4x \le \frac{1}{4} \cdot {\left( {\frac{{1 - 2x + 1 - 2x + 4x}}{3}} \right)^3} = \frac{2}{{27}}\)

Dấu "=" xảy ra khi \(1 - 2x = 4x \Leftrightarrow x = \frac{1}{6}\).

Vậy để thể tích chiếc thùng là lớn nhất thì các cạnh của hình vuông được cắt bỏ đi là \(\frac{1}{6}{\rm{\;m}}\).

Giải bài 7.40 trang 41 SBT Toán 11 Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu

Bài 7.40 trang 41 sách bài tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tìm điểm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:

Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần khảo sát.
Tính đạo hàm: Tính đạo hàm bậc nhất của hàm số.
Tìm điểm cực trị: Giải phương trình đạo hàm bằng 0 để tìm các điểm nghi ngờ là điểm cực trị.
Xác định loại điểm cực trị: Sử dụng dấu của đạo hàm bậc nhất hoặc đạo hàm bậc hai để xác định xem các điểm tìm được là điểm cực đại, cực tiểu hay điểm uốn.
Kết luận: Viết kết luận về các điểm cực trị của hàm số.

Phân tích chi tiết bài toán 7.40 SBT Toán 11 Kết nối tri thức

Bài toán 7.40 thường có dạng như sau: Cho hàm số y = f(x). Tìm các điểm cực trị của hàm số.

Để giải bài toán này, ta thực hiện các bước như đã nêu ở trên. Cụ thể:

Bước 1: Xác định hàm số y = f(x).
Bước 2: Tính đạo hàm y' = f'(x).
Bước 3: Giải phương trình f'(x) = 0 để tìm các nghiệm x₁, x₂, ...
Bước 4: Xét dấu của f'(x) trên các khoảng ( -∞; x₁), (x₁; x₂), ..., (x_n; +∞). Nếu f'(x) đổi dấu từ dương sang âm tại x_i thì x_i là điểm cực đại. Nếu f'(x) đổi dấu từ âm sang dương tại x_i thì x_i là điểm cực tiểu.
Bước 5: Tính giá trị của hàm số tại các điểm cực trị để tìm tọa độ của chúng.

Ví dụ minh họa giải bài 7.40 SBT Toán 11 Kết nối tri thức

Giả sử hàm số y = x³ - 3x² + 2. Ta thực hiện các bước sau:

Tính đạo hàm: y' = 3x² - 6x
Tìm điểm cực trị: Giải phương trình 3x² - 6x = 0, ta được x = 0 hoặc x = 2.
Xác định loại điểm cực trị:
- Với x < 0, y' > 0.
- Với 0 < x < 2, y' < 0.
- Với x > 2, y' > 0.
Vậy x = 0 là điểm cực đại và x = 2 là điểm cực tiểu.
Kết luận: Hàm số có điểm cực đại tại x = 0, y = 2 và điểm cực tiểu tại x = 2, y = -2.

Lưu ý khi giải bài tập về đạo hàm và ứng dụng

Nắm vững các công thức tính đạo hàm cơ bản.
Chú ý đến điều kiện xác định của hàm số.
Kiểm tra lại kết quả sau khi giải bài tập.
Luyện tập thường xuyên để nâng cao kỹ năng giải toán.

Tusach.vn hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin giải bài 7.40 trang 41 sách bài tập Toán 11 Kết nối tri thức và đạt kết quả tốt trong môn học. Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ!