Giải bài 7.13 trang 30 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.13 trang 30 SBT Toán 11 - Kết nối tri thức
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 7.13 trang 30 sách bài tập Toán 11 Kết nối tri thức. Bài giải bao gồm các bước thực hiện rõ ràng, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách bài tập Toán 11 Kết nối tri thức, hỗ trợ tối đa cho quá trình học tập của bạn.
Cho tứ diện \(ABCD\) có tất cả các cạnh bằng nhau và bằng \(a\).
Đề bài
Cho tứ diện \(ABCD\) có tất cả các cạnh bằng nhau và bằng \(a\). Tính côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(BCD\).
Phương pháp giải - Xem chi tiết
Phương pháp chung
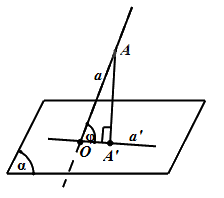
Để xác định góc giữa đường thẳng \(a\) và mặt phẳng \(\left( \alpha \right)\)ta thực hiện theo các bước sau:
- Tìm giao điểm \(O = a \cap \left( \alpha \right)\)
- Dựng hình chiếu \(A'\) của một điểm \(A \in a\) xuống \(\left( \alpha \right)\)
- Góc \(\widehat {AOA'} = \varphi \) chính là góc giữa đường thẳng \(a\) và \(\left( \alpha \right)\).
Gợi ý phương pháp giải
Kẻ \(AH \bot \left( {BCD} \right)\) tại \(H\),
Xác định hình chiếu của \(AB\) trên \(\left( {BCD} \right)\) là \(BH\)
Tính góc \(\left( {AB,BH} \right) = \widehat {ABH}\) rồi kết luận
Lời giải chi tiết
Kẻ \(AH \bot \left( {BCD} \right)\) tại \(H\), ta có \(BH\) là hình chiếu vuông góc của \(AB\) trên mặt phẳng \(\left( {BCD} \right)\) nên góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\) bằng góc giữa hai đường thẳng \(AB\) và \(BH\), mà \(\left( {AB,BH} \right) = \widehat {ABH}\).
Vì \(AB = AC = AD\) nên \(HB = HC = HD\), hay \(H\) là tâm của tam giác\(BCD\), suy ra\(BH = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\).
Từ đó ta tính được: \(\cos \widehat {ABH} = \frac{{BH}}{{AB}} = \frac{{\sqrt 3 }}{3}\).
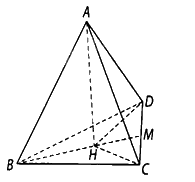
Vậy côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\) bằng \(\frac{{\sqrt 3 }}{3}\).
Giải bài 7.13 trang 30 SBT Toán 11 - Kết nối tri thức: Hướng dẫn chi tiết
Bài 7.13 trang 30 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng, giúp học sinh củng cố kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh xác định mối quan hệ giữa đường thẳng và mặt phẳng, tính góc giữa chúng, hoặc tìm giao điểm của đường thẳng và mặt phẳng.
Nội dung bài tập 7.13 trang 30 SBT Toán 11 - Kết nối tri thức
Bài tập 7.13 thường có dạng như sau:
- Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng AM và SD không cùng thuộc một mặt phẳng.
- Cho hình chóp S.ABCD. Gọi I là giao điểm của AC và BD. Chứng minh rằng SI vuông góc với mặt phẳng (ABCD).
- Cho hình chóp S.ABCD. Tính góc giữa đường thẳng SA và mặt phẳng (ABCD).
Phương pháp giải bài tập 7.13 trang 30 SBT Toán 11 - Kết nối tri thức
Để giải bài tập 7.13 trang 30 SBT Toán 11 Kết nối tri thức, học sinh cần nắm vững các kiến thức sau:
- Khái niệm về đường thẳng và mặt phẳng: Hiểu rõ định nghĩa, tính chất của đường thẳng và mặt phẳng.
- Mối quan hệ giữa đường thẳng và mặt phẳng: Biết cách xác định đường thẳng thuộc mặt phẳng, đường thẳng song song với mặt phẳng, đường thẳng vuông góc với mặt phẳng, đường thẳng cắt mặt phẳng.
- Góc giữa đường thẳng và mặt phẳng: Hiểu rõ định nghĩa, cách tính góc giữa đường thẳng và mặt phẳng.
- Các định lý về quan hệ song song và vuông góc trong không gian: Sử dụng các định lý để chứng minh các mối quan hệ giữa đường thẳng và mặt phẳng.
Lời giải chi tiết bài 7.13 trang 30 SBT Toán 11 - Kết nối tri thức (Ví dụ)
Bài toán: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh BC. Chứng minh rằng AM và SD không cùng thuộc một mặt phẳng.
Lời giải:
Giả sử AM và SD cùng thuộc một mặt phẳng (α). Khi đó, mặt phẳng (α) chứa hai đường thẳng AM và SD. Vì AM thuộc mặt phẳng (ABC) và SD thuộc mặt phẳng (SCD), nên mặt phẳng (α) chứa giao tuyến của hai mặt phẳng (ABC) và (SCD), tức là đường thẳng AC. Tương tự, mặt phẳng (α) cũng chứa giao tuyến của (ABM) và (SCD), là một đường thẳng khác. Điều này dẫn đến việc mặt phẳng (α) phải chứa ít nhất ba điểm không thẳng hàng A, C, và một điểm trên giao tuyến của (ABM) và (SCD). Tuy nhiên, điều này mâu thuẫn với giả thiết rằng AM và SD không cùng thuộc một mặt phẳng. Do đó, AM và SD không cùng thuộc một mặt phẳng.
Lưu ý khi giải bài tập 7.13 trang 30 SBT Toán 11 - Kết nối tri thức
- Vẽ hình chính xác và rõ ràng.
- Sử dụng các định lý và tính chất một cách linh hoạt.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin giải quyết bài tập 7.13 trang 30 SBT Toán 11 Kết nối tri thức một cách hiệu quả. Chúc các bạn học tốt!
| Chủ đề | Nội dung |
|---|---|
| Đường thẳng và mặt phẳng | Khái niệm, tính chất, mối quan hệ |
| Góc giữa đường thẳng và mặt phẳng | Định nghĩa, cách tính |
| Ứng dụng | Giải bài tập trong sách bài tập |