Giải bài 7.29 trang 38 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.29 trang 38 SBT Toán 11 Kết nối tri thức
Tusach.vn xin giới thiệu đáp án chi tiết bài 7.29 trang 38 Sách bài tập Toán 11 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
Chúng tôi cung cấp lời giải dễ hiểu, phương pháp giải rõ ràng, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\)
Đề bài
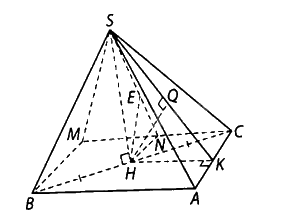
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), góc \(ABC\) bằng \({60^ \circ }\), biết tam giác \(SBC\) đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng \(\left( {ABC} \right)\). Tính theo a khoảng cách:
a) Từ điểm \(S\) đến mặt phẳng \(\left( {ABC} \right)\).
b) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
c) Giữa hai đường thẳng \(AB\) và \(SC\).
Phương pháp giải - Xem chi tiết
a) Tính khoảng cách từ điểm \(S\) đến mặt phẳng \(\left( {ABC} \right)\).
Bước 1: Kẻ \(SH\) vuông góc với \(BC\) tại \(H\)
Do \(\left( {SBC} \right) \bot \left( {ABC} \right) \Rightarrow SH \bot \left( {ABC} \right)\)
\( \Rightarrow d\left( {S,\left( {ABC} \right)} \right) = SH\)
Bước 2: Tính \(SH\)
b) Tính khoảng cách từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
Bước 1: Tính khoảng cách từ \(H\) đến mặt phẳng \(\left( {SAC} \right)\).
Bước 2: Nhận xét \(H\) là trung điểm của \(BC\) nên \(d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right)\)c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(SC\).
Bước 1: Dựng hình bình hành \(ABMC\), chứng minh được \(ABMC\) là hình chữ nhật.
Khi đó \(AB//\left( {SCM} \right)\) và mặt phẳng \(\left( {SMC} \right)\) chứa \(SC\) nên
\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = d\left( {B,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)
Bước 2: Tính \(\left( {H,\left( {SCM} \right)} \right) \Rightarrow \)\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)
Lời giải chi tiết
a) Kẻ \(SH\) vuông góc với \(BC\) tại \(H\) thì \(SH \bot \left( {ABC} \right)\), suy ra \(d\left( {S,\left( {ABC} \right)} \right) = SH = \frac{{a\sqrt 3 }}{2}\)
b) Kẻ HK vuông góc với \(AC\) tại \(K,HQ\) vuông góc với \(SK\) tại \(Q\) thì \(d\left( {H,\left( {SAC} \right)} \right) = HQ\).
Ta có: \(AB = \frac{a}{2},HK = \frac{a}{4}\) và tam giác \(SHK\) vuông tại \(H\), đường cao \(HQ\) nên \(HQ = \frac{{SH \cdot HK}}{{SK}} = \frac{{a\sqrt {39} }}{{26}}\).
Lại có \(H\) là trung điểm của \(BC\) nên \(d\left( {B,\left( {SAC} \right)} \right) = 2d\left( {H,\left( {SAC} \right)} \right) = \frac{{a\sqrt {39} }}{{13}}\).
c) Dựng hình bình hành \(ABMC\), chứng minh được \(ABMC\) là hình chữ nhật.
Khi đó \(AB//\left( {SCM} \right)\) và mặt phẳng \(\left( {SMC} \right)\) chứa \(SC\) nên
\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCM} \right)} \right) = d\left( {B,\left( {SCM} \right)} \right) = 2d\left( {H,\left( {SCM} \right)} \right){\rm{.\;}}\)
Kẻ \(HN\) vuông góc với \(CM\) tại \(N,HE\) vuông góc với \(SN\) tại \(N\) thì \(HE \bot \left( {SCM} \right)\), suy ra \(d\left( {H,\left( {SCM} \right)} \right) = HE\).
Ta có: \(HN = \frac{{BM}}{2} = \frac{{a\sqrt 3 }}{4}\), tam giác SHN vuông tại \(H\), đường cao \(HE\) nên \(HE = \frac{{SH \cdot HN}}{{SN}} = \frac{{a\sqrt {15} }}{{10}}\).
Vậy \(d\left( {AB,SC} \right) = \frac{{a\sqrt {15} }}{5}\).
Giải bài 7.29 trang 38 SBT Toán 11 Kết nối tri thức: Chi tiết và Dễ hiểu
Bài 7.29 trang 38 Sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Dưới đây là lời giải chi tiết và phương pháp giải bài tập này:
Đề bài:
Cho hàm số y = f(x) có đạo hàm f'(x) = (x-1)^2(x+3). Hỏi hàm số y = f(x) đồng biến trên khoảng nào?
Lời giải:
Để hàm số y = f(x) đồng biến trên một khoảng, cần có f'(x) > 0. Ta xét dấu của f'(x) = (x-1)^2(x+3):
- (x-1)^2 ≥ 0 với mọi x
- x + 3 > 0 khi x > -3
Vậy, f'(x) > 0 khi x > -3 và x ≠ 1. Do đó, hàm số y = f(x) đồng biến trên các khoảng (-3; 1) và (1; +∞).
Phương pháp giải:
Để giải bài toán này, chúng ta cần nắm vững các kiến thức sau:
- Định nghĩa đạo hàm: f'(x) là đạo hàm của hàm số y = f(x) tại điểm x.
- Điều kiện đồng biến: Hàm số y = f(x) đồng biến trên khoảng (a; b) khi và chỉ khi f'(x) > 0 với mọi x thuộc (a; b).
- Xét dấu tam thức bậc hai: Trong trường hợp này, f'(x) là một tam thức bậc hai, do đó chúng ta cần xét dấu của nó để xác định khoảng mà f'(x) > 0.
Lưu ý quan trọng:
Khi xét dấu của đạo hàm, cần chú ý đến các điểm mà đạo hàm bằng 0 hoặc không xác định. Tại các điểm này, hàm số có thể không đồng biến hoặc nghịch biến.
Bài tập tương tự:
Để rèn luyện thêm kỹ năng giải các bài tập về đạo hàm và ứng dụng của đạo hàm, các em có thể tham khảo các bài tập sau:
- Bài 7.30 trang 38 SBT Toán 11 Kết nối tri thức
- Bài 7.31 trang 39 SBT Toán 11 Kết nối tri thức
Kết luận:
Bài 7.29 trang 38 SBT Toán 11 Kết nối tri thức là một bài tập điển hình về ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp các em học sinh tự tin hơn trong quá trình học tập và làm bài kiểm tra.
Tusach.vn hy vọng rằng lời giải chi tiết và phương pháp giải bài tập này sẽ giúp các em học sinh hiểu rõ hơn về bài học và đạt kết quả tốt trong môn Toán 11.
| Khái niệm | Giải thích |
|---|---|
| Đạo hàm | Tốc độ thay đổi tức thời của hàm số tại một điểm. |
| Đồng biến | Hàm số tăng khi biến độc lập tăng. |
| Nghịch biến | Hàm số giảm khi biến độc lập tăng. |
| Nguồn: Tusach.vn | |