Đề bài
Cho hình chóp \(S.ABCD\)có tất cả các cạnh đều bằng \(a\), gọi \(O\)là giao điểm của \(AC\) và \(BD\). Khoảng cách giữa hai đường thẳng \(AB\) và \(SD\) bằng
A. \(\frac{{a\sqrt 6 }}{3}\).
B. \(\frac{{a\sqrt 3 }}{2}\).
C. .\(\frac{{a\sqrt 6 }}{3}\).
D. \(\frac{{a\sqrt 6 }}{2}\).
Phương pháp giải - Xem chi tiết
Gọi \(M,N\) lần lượt là trung điểm của các cạnh\(AB,CD\); \(H\) là hình chiếu vuông góc của \(O\) trên \(SN.\)
Vì \(AB{\rm{//}}CD\) nên\(d\left( {AB,SD} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\)
Ta có \(\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH\)
Khi đó \(\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.\)
Tam giác \(SOD\) vuông tại \(O\) nên \(O{S^2} = S{D^2} - O{D^2}\)
Tam giác \(SON\) vuông tại \(O\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{S^2}}} \Rightarrow OH\)
Vậy \(d\left( {AB,SD} \right) = 2OH\).
Lời giải chi tiết
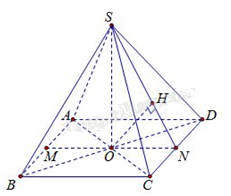
Gọi \(M,N\) lần lượt là trung điểm của các cạnh\(AB,CD\); \(H\) là hình chiếu vuông góc của \(O\) trên \(SN.\)
Vì \(AB{\rm{//}}CD\) nên \(d\left( {AB,SD} \right) = d\left( {AB,(SCD)} \right) = d\left( {M,(SCD)} \right) = 2d\left( {O,(SCD)} \right)\)
Ta có \(\left\{ \begin{array}{l}CD \bot SO\\CD \bot ON\end{array} \right. \Rightarrow CD \bot (SON) \Rightarrow CD \bot OH\)
Khi đó \(\left\{ \begin{array}{l}CD \bot OH\\OH \bot SN\end{array} \right. \Rightarrow OH \bot (SCD) \Rightarrow d\left( {O;(SCD)} \right) = OH.\)
Tam giác \(SOD\) vuông tại \(O\) nên \(O{S^2} = S{D^2} - O{D^2} = {a^2} - {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{{a^2}}}{2}\)
Tam giác \(SON\) vuông tại \(O\) nên \(\frac{1}{{O{H^2}}} = \frac{1}{{O{N^2}}} + \frac{1}{{O{S^2}}} = \frac{1}{{\frac{{{a^2}}}{4}}} + \frac{1}{{\frac{{{a^2}}}{2}}} = \frac{6}{{{a^2}}} \Rightarrow OH = \frac{a}{{\sqrt 6 }} = \frac{{a\sqrt 6 }}{6}\)
Vậy \(d\left( {AB,SD} \right) = 2OH = \frac{{a\sqrt 6 }}{3}\).
