Giải bài 19 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 19 trang 69 SBT Toán 11 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 19 trang 69 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án, cách giải và những lưu ý quan trọng để các em hiểu rõ hơn về nội dung bài học.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho hình lập phương (ABCD cdot A'B'C'D') có cạnh bằng (a). Góc giữa hai đường thẳng (AC) và (BC') bằng
Đề bài
Cho hình lập phương \(ABCD \cdot A'B'C'D'\) có cạnh bằng \(a\). Góc giữa hai đường thẳng \(AC\) và \(BC'\) bằng
A. \({90^ \circ }\).
B. \({30^ \circ }\).
C. \({60^ \circ }\).
D. \({45^ \circ }\).
Phương pháp giải - Xem chi tiết
Phương pháp
Ta có \(AC//A'C' \Rightarrow \left( {AC,BC'} \right) = \left( {A'C',BC'} \right)\)
Nhận dạng tam giác \(BA'C'\) đều \( \Rightarrow \left( {A'C',BC'} \right) = {60^ \circ }\)
Lời giải chi tiết
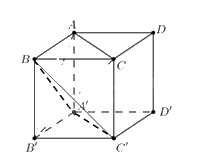
Ta có \(AC//A'C' \Rightarrow \left( {AC,BC'} \right) = \left( {A'C',BC'} \right)\)
Xét tam giác \(BA'C'\) có ba cạnh là ba đường chéo của 3 hình vuông bằng nhau nên tam giác \(BA'C'\) đều. Vậy \(\left( {AC,BC'} \right) = \left( {A'C',BC'} \right) = {60^ \circ }\)
Chọn C
Giải bài 19 trang 69 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 19 trang 69 sách bài tập Toán 11 Kết nối tri thức tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập bao gồm các dạng bài tập về xác định tập xác định của hàm số, tìm tập giá trị, xét tính đơn điệu, tìm cực trị và vẽ đồ thị hàm số lượng giác. Việc nắm vững kiến thức về hàm số lượng giác là nền tảng quan trọng để giải quyết các bài toán liên quan trong chương trình học.
Nội dung chi tiết bài 19 trang 69 SBT Toán 11 - Kết nối tri thức
Bài 19 bao gồm nhiều câu hỏi nhỏ, mỗi câu hỏi tập trung vào một khía cạnh khác nhau của hàm số lượng giác. Dưới đây là giải chi tiết từng câu hỏi:
Câu 1: Xác định tập xác định của hàm số
Để xác định tập xác định của hàm số lượng giác, cần lưu ý các điều kiện sau:
- Mẫu số khác 0
- Biểu thức dưới dấu căn bậc chẵn lớn hơn hoặc bằng 0
- Biểu thức trong logarit lớn hơn 0
Ví dụ: Hàm số y = 1/(sin x - cos x) có tập xác định là tập hợp tất cả các giá trị x sao cho sin x - cos x ≠ 0.
Câu 2: Tìm tập giá trị của hàm số
Tập giá trị của hàm số lượng giác là tập hợp tất cả các giá trị mà hàm số có thể nhận được. Để tìm tập giá trị, có thể sử dụng các phương pháp sau:
- Sử dụng tính chất của hàm số lượng giác (ví dụ: -1 ≤ sin x ≤ 1, -1 ≤ cos x ≤ 1)
- Biến đổi hàm số về dạng đơn giản hơn
- Sử dụng đạo hàm để tìm cực trị của hàm số
Ví dụ: Hàm số y = 2sin x + 1 có tập giá trị là [-1, 3].
Câu 3: Xét tính đơn điệu của hàm số
Để xét tính đơn điệu của hàm số, có thể sử dụng đạo hàm của hàm số:
- Nếu đạo hàm f'(x) > 0 trên một khoảng, hàm số đồng biến trên khoảng đó.
- Nếu đạo hàm f'(x) < 0 trên một khoảng, hàm số nghịch biến trên khoảng đó.
Ví dụ: Hàm số y = cos x nghịch biến trên khoảng (0, π).
Câu 4: Tìm cực trị của hàm số
Cực trị của hàm số là các điểm mà tại đó hàm số đạt giá trị lớn nhất hoặc nhỏ nhất. Để tìm cực trị, cần giải phương trình f'(x) = 0 và xét dấu của đạo hàm cấp hai f''(x):
- Nếu f'(x) = 0 và f''(x) > 0, hàm số đạt cực tiểu tại x.
- Nếu f'(x) = 0 và f''(x) < 0, hàm số đạt cực đại tại x.
Ví dụ: Hàm số y = sin x đạt cực đại tại x = π/2 và cực tiểu tại x = 3π/2.
Lưu ý khi giải bài tập
Khi giải bài tập về hàm số lượng giác, cần lưu ý những điều sau:
- Nắm vững các công thức lượng giác cơ bản.
- Sử dụng các phương pháp biến đổi lượng giác để đơn giản hóa bài toán.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Kết luận
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh có thể tự tin giải quyết bài 19 trang 69 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
| tan x = sin x / cos x | Định nghĩa hàm tan |