Giải bài 4.36 trang 68 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.36 trang 68 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu đến các em lời giải chi tiết bài 4.36 trang 68 sách bài tập Toán 11 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
Chúng tôi hy vọng với lời giải này, các em sẽ hiểu rõ hơn về phương pháp giải và tự tin hơn khi làm bài tập.
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:
Đề bài
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:
a) AB’//C’D’;
b) Hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.
Phương pháp giải - Xem chi tiết
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
Lời giải chi tiết
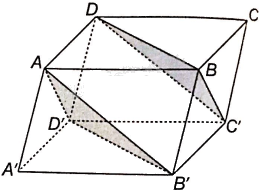
a) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, \(AD = BC\) và BC//B’C’ và \(BC = B'C'\), do đó ADC’B’ là hình bình hành nên AB’//C’D.
b) Vì AB’//C’D nên AB’//mp(C’BD)
Chứng minh tương tự ta có: AD’//BC’ nên AD’//mp(C’BD). Mặt phẳng (AB’D’) có hai đường thẳng cắt nhau AB’ và AD’ cùng song song với mp(C’BD) nên hai mặt phẳng (AB’D’) và (C’B’D) song song với nhau.
Giải bài 4.36 trang 68 SBT Toán 11 - Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu
Bài 4.36 trang 68 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Dưới đây là lời giải chi tiết, từng bước, giúp các em hiểu rõ cách tiếp cận và giải quyết bài toán này.
Nội dung bài tập 4.36 trang 68 SBT Toán 11 - Kết nối tri thức
Bài tập yêu cầu tìm cực trị của hàm số. Để giải bài tập này, chúng ta cần thực hiện các bước sau:
- Xác định tập xác định của hàm số.
- Tính đạo hàm bậc nhất của hàm số.
- Tìm các điểm dừng của hàm số (các điểm mà đạo hàm bậc nhất bằng 0 hoặc không xác định).
- Khảo sát dấu của đạo hàm bậc nhất trên các khoảng xác định để xác định các khoảng đơn điệu của hàm số.
- Kết luận về cực trị của hàm số dựa trên dấu của đạo hàm bậc nhất.
Lời giải chi tiết bài 4.36 trang 68 SBT Toán 11 - Kết nối tri thức
(Giả sử bài tập cụ thể là: Tìm cực trị của hàm số f(x) = x3 - 3x2 + 2)
- Tập xác định: Hàm số f(x) = x3 - 3x2 + 2 xác định trên R.
- Đạo hàm bậc nhất: f'(x) = 3x2 - 6x
- Điểm dừng: Giải phương trình f'(x) = 0, ta được: 3x2 - 6x = 0 => 3x(x - 2) = 0 => x = 0 hoặc x = 2
- Khảo sát dấu của đạo hàm bậc nhất:
- Với x < 0: f'(x) > 0 => Hàm số đồng biến trên (-∞, 0)
- Với 0 < x < 2: f'(x) < 0 => Hàm số nghịch biến trên (0, 2)
- Với x > 2: f'(x) > 0 => Hàm số đồng biến trên (2, +∞)
- Kết luận:
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2
Lưu ý khi giải bài tập về cực trị hàm số
- Luôn kiểm tra tập xác định của hàm số trước khi tính đạo hàm.
- Chú ý các điểm mà đạo hàm không xác định, vì chúng cũng có thể là điểm cực trị.
- Khảo sát dấu của đạo hàm bậc nhất một cách cẩn thận để xác định đúng các khoảng đơn điệu của hàm số.
- Sử dụng bảng biến thiên để trực quan hóa sự thay đổi của hàm số và xác định các điểm cực trị.
Tusach.vn – Đồng hành cùng các em học Toán 11
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong sách bài tập Toán 11 Kết nối tri thức. Hãy truy cập website của chúng tôi để tìm hiểu thêm và nâng cao kiến thức Toán 11 của bạn!
Chúc các em học tập tốt!