Giải bài 7.5 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.5 trang 26 SBT Toán 11 Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 7.5 trang 26 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án, cách giải và giải thích chi tiết từng bước để giúp các em hiểu rõ hơn về nội dung bài học.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
Một chiếc thang có dạng hình thang cân cao (6{rm{;m}}), hai chân thang cách nhau (80{rm{;cm}})
Đề bài
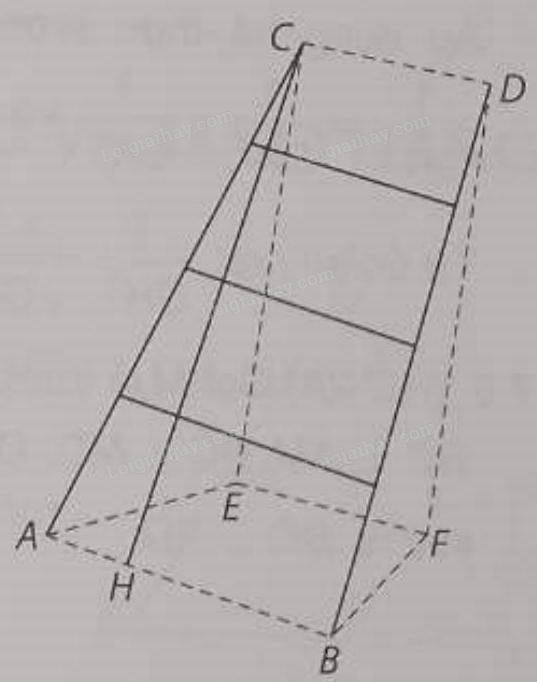
Một chiếc thang có dạng hình thang cân cao \(6{\rm{\;m}}\), hai chân thang cách nhau \(80{\rm{\;cm}}\), hai ngọn thang cách nhau \(60{\rm{\;cm}}\).Thang được dựa vào bờ tường như hình bên. Tính góc tạo giữa đường thẳng chân tường và cạnh cột thang (tính gần đúng theo đơn vị độ, làm tròn kết quả đến chữ số thập phân thứ hai).

Phương pháp giải - Xem chi tiết
Gọi A, B là hai điểm tại hai vị tri chân thang và C, D là hai điểm tại hai vị trí ngọn thang, EF là đường chân tường. Khi đó, chân tường là EF, cột thang là AC.
Ta có EF // AB nên \(\left( {EF,AC} \right) = \left( {AB,AC} \right) = \widehat {BAC}\).
Kẻ CH vuông góc với AB tại H, tính \(AH = \frac{{AB - CD}}{2}\).
Tam giác ACH vuông tại H nên tính được \({\rm{cos}}\widehat {CAH}\), suy ra \(\widehat {CAH}\).
Lời giải chi tiết
Gọi A, B là hai điểm tại hai vị tri chân thang và C, D là hai điểm tại hai vị trí ngọn thang, EF là đường chân tường. Khi đó, chân tường là EF, cột thang là AC.
Ta có EF // AB nên \(\left( {EF,AC} \right) = \left( {AB,AC} \right) = \widehat {BAC}\).
Kẻ \(CH\) vuông góc với \(AB\) tại \(H\), khi đó \(AH = \frac{{AB - CD}}{2} = 10\left( {{\rm{\;cm}}} \right) = 0,1\left( {{\rm{\;m}}} \right)\).
Tam giác \(ACH\) vuông tại \(H\) nên \({\rm{cos}}\widehat {CAH} = \frac{{AH}}{{AC}} = \frac{{0,1}}{6} = \frac{1}{{60}}\), suy ra \(\widehat {CAH} \approx 89,{05^ \circ }\).
Vậy góc tạo giữa đường thẳng chân tường và cạnh cột thang bằng khoảng \(89,{05^ \circ }\).
Giải bài 7.5 trang 26 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp giải
Bài 7.5 trang 26 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Nội dung chính của bài 7.5 trang 26 SBT Toán 11 Kết nối tri thức
- Tính đạo hàm của các hàm số lượng giác (sin, cos, tan, cot).
- Vận dụng quy tắc đạo hàm của hàm hợp.
- Giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
Hướng dẫn giải chi tiết bài 7.5 trang 26 SBT Toán 11 Kết nối tri thức
Để giải bài 7.5 trang 26 SBT Toán 11 Kết nối tri thức một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Công thức đạo hàm cơ bản: (sin x)' = cos x, (cos x)' = -sin x, (tan x)' = 1/cos2x, (cot x)' = -1/sin2x
- Quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x)
- Các kỹ năng biến đổi đại số: Để đơn giản hóa biểu thức trước khi tính đạo hàm.
Ví dụ minh họa giải bài 7.5 trang 26 SBT Toán 11 Kết nối tri thức
Bài toán: Tính đạo hàm của hàm số y = sin(2x + 1)
Lời giải:
Đặt u = 2x + 1, khi đó y = sin(u)
Ta có: u' = 2 và y' = cos(u)
Áp dụng quy tắc đạo hàm của hàm hợp, ta được:
y' = cos(u) * u' = cos(2x + 1) * 2 = 2cos(2x + 1)
Các dạng bài tập thường gặp trong bài 7.5 trang 26 SBT Toán 11 Kết nối tri thức
- Dạng 1: Tính đạo hàm của hàm số lượng giác đơn giản.
- Dạng 2: Tính đạo hàm của hàm hợp chứa hàm lượng giác.
- Dạng 3: Tìm đạo hàm cấp hai của hàm số.
- Dạng 4: Ứng dụng đạo hàm để giải các bài toán liên quan đến cực trị, khoảng đơn điệu của hàm số.
Lưu ý khi giải bài tập về đạo hàm
- Luôn kiểm tra lại các công thức đạo hàm cơ bản.
- Sử dụng quy tắc đạo hàm của hàm hợp một cách chính xác.
- Biến đổi biểu thức một cách cẩn thận để tránh sai sót.
- Kiểm tra lại kết quả bằng cách thay các giá trị cụ thể vào hàm số và đạo hàm.
Tusach.vn - Nguồn tài liệu học tập Toán 11 uy tín
Tusach.vn cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm:
- Giải bài tập sách giáo khoa
- Giải bài tập sách bài tập
- Đề thi thử Toán 11
- Các bài viết hướng dẫn, tổng hợp kiến thức
Hãy truy cập Tusach.vn để đồng hành cùng các em trên con đường chinh phục môn Toán!
| Công thức | Mô tả |
|---|---|
| (sin x)' | Đạo hàm của sin x bằng cos x |
| (cos x)' | Đạo hàm của cos x bằng -sin x |