Đề bài
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\). \(SA \bot \left( {ABC} \right)\) và \(SA = 2a\)
Tính theo \(a\) khoảng cách
a) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
b) Từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\).
c) Giữa hai đường thẳng \(AB\) và \(SC\).
Phương pháp giải - Xem chi tiết
a) Từ điểm \(B\) đến mặt phẳng \(\left( {SAC} \right)\).
Bước 1: Xác định hình chiếu vuông góc của lên mặt phẳng là \(H\)
Bước 2: Tính \(BH\).
a) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\).
Bước 1: Xác định hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( {SBC} \right)\) là \(K\)
Bước 2: Tính \(AK\).
c) Tính khoảng cách từ giữa hai đường thẳng \(AB\) và \(SC\).
Bước 1: Dựng mặt phẳng \(\left( {SCD} \right)\) chứa \(SC\) và song song với \(AB\)
Dựng hình bình hành \(ABCD\) thì \(AB//\left( {SCD} \right)\) và mặt phẳng \(\left( {SCD} \right)\) chứa \(SC\) nên \(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right)\). Mà \(d\left( {AB,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right)\)
Bước 2: Tính \(d\left( {A,\left( {SCD} \right)} \right)\).
Kết luận \(d\left( {AB,SC} \right)\).
Lời giải chi tiết
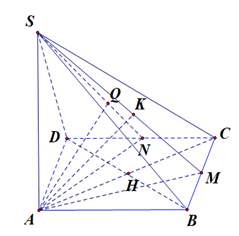
a) Kẻ \(BH \bot AC\) tại \(H\), mà \(SA \bot \left( {ABC} \right)\) nên \(SA \bot BH\), suy ra \(BH \bot \left( {SAC} \right)\).
Do đó, \(d\left( {B,\left( {SAC} \right)} \right) = BH = \frac{{a\sqrt 3 }}{2}\).
b) Kẻ \(AM \bot BC\) tại \(M\) và \(AK \bot SM\) tại \(K\) thì \(AK \bot \left( {SBC} \right)\), suy ra \(d\left( {A,\left( {SBC} \right)} \right) = AK\).
Ta có: \(\frac{1}{{A{K^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}} = \frac{{19}}{{12{a^2}}} \Rightarrow AK = 2{\rm{a}}\sqrt {\frac{3}{{19}}} \). Nên \(d\left( {A,\left( {SBC} \right)} \right) = 2{\rm{a}}\sqrt {\frac{3}{{19}}} \).
c) Dựng hình bình hành \(ABCD\) thì \(AB\parallel \left( {SCD} \right)\) và mặt phẳng \(\left( {SCD} \right)\) chứa \(SC\) nên\(d\left( {AB,SC} \right) = d\left( {AB,\left( {SCD} \right)} \right)\).
Mà \(d\left( {AB,\left( {SCD} \right)} \right) = d\left( {A,\left( {SCD} \right)} \right)\), tính tương tự câu b) ta được
\(d\left( {A,\left( {SCD} \right)} \right) = 2{\rm{a}}\sqrt {\frac{3}{{19}}} \). Vậy \(d\left( {AB,SC} \right) = 2{\rm{a}}\sqrt {\frac{3}{{19}}} \).
