Giải bài 7.16 trang 31 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.16 trang 31 SBT Toán 11 - Kết nối tri thức
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 7.16 trang 31 sách bài tập Toán 11 Kết nối tri thức. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập tốt nhất, hỗ trợ học sinh ôn tập và làm bài tập hiệu quả.
Cho hình hộp \(ABCD \cdot A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh a và \(AA' = a\sqrt 2 \)
Đề bài
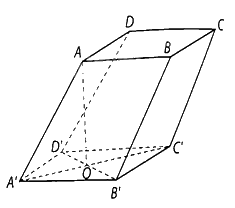
Cho hình hộp \(ABCD \cdot A'B'C'D'\) có đáy \(ABCD\) là hình vuông cạnh a và \(AA' = a\sqrt 2 \), hình chiếu vuông góc của \(A\) trên mặt phẳng \(\left( {A'B'C'D'} \right)\) trùng với trung điểm của \(B'D'\). Tính góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {A'B'C'D'} \right)\).
Phương pháp giải - Xem chi tiết
Gọi \(O\) là giao điểm của \(A'C'\) và \(B'D'\)
Xác định hình chiếu vuông góc của \(AA'\) trên mặt phẳng \(\left( {A'B'CD'} \right)\)
Tính góc giữa đường thẳng \(AA'\) và hình chiếu của nó rồi kết luận
Áp dụng tỉ số lượng giác cho tam giác vuông để tính góc
Lời giải chi tiết
Gọi \(O\) là giao điểm của \(A'C'\) và \(B'D'\).
Ta có: \(A'O\) là hình chiếu vuông góc của \(AA'\) trên mặt phẳng \(\left( {A'B'CD'} \right)\), góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {A'B'C'D'} \right)\) bằng góc giữa \(AA'\) và \(A'O\).
Mà \(\left( {AA',A'O} \right) = \widehat {AA'O}\), ta lại có \(A'O = \frac{{a\sqrt 2 }}{2}\).
Do đó \({\rm{cos}}\widehat {AA'O} = \frac{{OA'}}{{AA'}} = \frac{1}{2}\),
Suy ra \(\widehat {AA'O} = {60^ \circ }\).
Vậy góc giữa đường thẳng \(AA'\) và mặt phẳng \(\left( {A'B'C'D'} \right)\) bằng \({60^ \circ }\).
Giải bài 7.16 trang 31 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp giải
Bài 7.16 trang 31 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về phép biến hình. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán liên quan đến hình học.
Nội dung bài tập 7.16 trang 31 SBT Toán 11
Bài tập 7.16 thường bao gồm các dạng bài sau:
- Xác định ảnh của một điểm, một đường thẳng hoặc một hình qua một phép biến hình.
- Tìm tâm, trục hoặc góc của một phép biến hình.
- Chứng minh một hình là ảnh của một hình khác qua một phép biến hình.
- Ứng dụng các phép biến hình để giải quyết các bài toán hình học.
Phương pháp giải bài tập 7.16 trang 31 SBT Toán 11
Để giải quyết bài tập 7.16 trang 31 SBT Toán 11 hiệu quả, học sinh cần nắm vững các kiến thức sau:
- Khái niệm về phép biến hình: Hiểu rõ định nghĩa, tính chất của từng loại phép biến hình (tịnh tiến, quay, đối xứng trục, đối xứng tâm).
- Biểu thức của phép biến hình: Nắm vững công thức biểu diễn phép biến hình trong hệ tọa độ.
- Tính chất bảo toàn của phép biến hình: Biết phép biến hình bảo toàn khoảng cách, góc và diện tích.
- Ứng dụng các phép biến hình: Sử dụng các phép biến hình để giải quyết các bài toán hình học một cách sáng tạo.
Lời giải chi tiết bài 7.16 trang 31 SBT Toán 11 - Kết nối tri thức
(Ở đây sẽ là lời giải chi tiết của bài tập 7.16, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)
Bài 7.16: Cho điểm A(1; 2) và đường thẳng d: x + y - 3 = 0. Tìm ảnh của điểm A và đường thẳng d qua phép tịnh tiến theo vectơ v = (2; -1).
Giải:
- Ảnh của điểm A: Gọi A' là ảnh của A qua phép tịnh tiến theo vectơ v. Khi đó, tọa độ của A' là: A'(1 + 2; 2 - 1) = A'(3; 1).
- Ảnh của đường thẳng d: Gọi d' là ảnh của d qua phép tịnh tiến theo vectơ v. Mỗi điểm M(x; y) thuộc d sẽ được chuyển thành điểm M'(x + 2; y - 1) thuộc d'. Thay x = x' - 2 và y = y' + 1 vào phương trình d, ta được: (x' - 2) + (y' + 1) - 3 = 0 ⇔ x' + y' - 4 = 0. Vậy phương trình của d' là: x + y - 4 = 0.
Luyện tập thêm các bài tập tương tự
Để củng cố kiến thức và kỹ năng giải bài tập về phép biến hình, học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi làm bài thi.
Tusach.vn - Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn luôn đồng hành cùng học sinh trong quá trình học tập. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các phương pháp giải bài tập hiệu quả. Hãy truy cập Tusach.vn để được hỗ trợ tốt nhất!
| Phép biến hình | Công thức |
|---|---|
| Tịnh tiến | x' = x + a, y' = y + b |
| Quay | x' = xcosα - ysinα, y' = xsinα + ycosα |