Giải bài 7.4 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.4 trang 26 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 7.4 trang 26 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học tập tốt hơn.
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) và tất cả các cạnh của hình chóp đều bằng a.
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình vuông tâm \(O\) và tất cả các cạnh của hình chóp đều bằng a. Gọi \(M\), N lần lượt là trung điểm các cạnh \(SA,AB\)
a) Tính góc giữa các cặp đường thẳng sau: \(MN\) và \(SD;MO\) và \(SB\)
b) Tính tang của góc giữa hai đường thẳng \(SN\) và \(BC\).
Phương pháp giải - Xem chi tiết
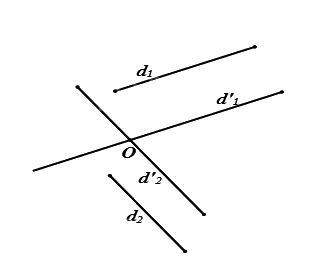
Từ \(O\) dựng các đường thẳng \(d'_1,d'_2\) lần lượt song song có thể trùng nếu \(O\) nằm trên một trong hai đường thẳngvới \({d_1}\) và \({d_2}\). Góc giữa hai đường thẳng \(d'_1,d'_2\)chính là góc giữa hai đường thẳng\({d_1},{d_2}\).
Lưu ý :
Áp dụng định lý Pytago đảo để chứng minh tam giác vuông
Áp dụng tính chất đường trung bình tam giác
Áp dụng tính chất \(\left\{ \begin{array}{l}a//b\\a \bot c\end{array} \right. \Rightarrow b \bot c\)
Lời giải chi tiết
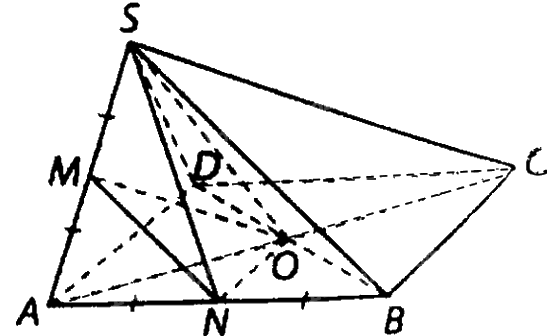
a) Ta có: \(B{D^2} = S{B^2} + S{D^2} = 2{a^2}\) nên \(\Delta SBD\) vuông tại \(S\), mà \(MN//SB\), suy ra \(\left( {MN,SD} \right) = \left( {SB,SD} \right) = {90^ \circ }\).
Với O là giao điểm của \(AC\) và \(BD\) thì \(MO//SC\).
Khi đó \(\left( {MO,SB} \right) = \left( {SC,SB} \right) = \widehat {BSC} = {60^ \circ }\).
b) Vì \(ON{\rm{ }}//BC\) nên \(\left( {SN,BC} \right) = \left( {SN,ON} \right) = \widehat {SNO}\).
Ta có \(SO = \frac{{a\sqrt 2 }}{2};ON = \frac{a}{2}\) và tam giác \(SNO\)vuông tại O nên \({\rm{tan}}\widehat {SNO} = \frac{{SO}}{{ON}} = \sqrt 2 \).
Vậy \({\rm{tan}}\left( {SN,BC} \right) = \sqrt 2 \).
Giải bài 7.4 trang 26 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp
Bài 7.4 trang 26 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Nội dung chính của bài 7.4
- Tính đạo hàm của hàm số tại một điểm.
- Tìm đạo hàm của hàm số.
- Vận dụng đạo hàm để giải các bài toán liên quan đến tiếp tuyến của đồ thị hàm số.
- Khảo sát hàm số bằng đạo hàm (xác định khoảng đồng biến, nghịch biến, cực trị).
Hướng dẫn giải chi tiết bài 7.4 trang 26 SBT Toán 11 - Kết nối tri thức
Để giải bài 7.4 trang 26 SBT Toán 11 Kết nối tri thức một cách hiệu quả, các em cần nắm vững các bước sau:
- Xác định hàm số: Đọc kỹ đề bài để xác định chính xác hàm số cần tính đạo hàm hoặc khảo sát.
- Chọn công thức đạo hàm phù hợp: Dựa vào dạng của hàm số, chọn công thức đạo hàm tương ứng (đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...).
- Tính đạo hàm: Áp dụng công thức đạo hàm đã chọn để tính đạo hàm của hàm số.
- Kiểm tra kết quả: Kiểm tra lại kết quả tính đạo hàm để đảm bảo tính chính xác.
- Vận dụng đạo hàm: Sử dụng đạo hàm để giải quyết các bài toán cụ thể (tìm tiếp tuyến, khảo sát hàm số,...).
Ví dụ minh họa (giả định bài tập cụ thể):
Bài tập: Tìm đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Các dạng bài tập thường gặp trong bài 7.4
- Dạng 1: Tính đạo hàm của hàm số đơn giản (đa thức, phân thức).
- Dạng 2: Tính đạo hàm của hàm hợp.
- Dạng 3: Tìm phương trình tiếp tuyến của đồ thị hàm số.
- Dạng 4: Khảo sát hàm số bằng đạo hàm.
Lưu ý khi giải bài tập về đạo hàm
Để tránh sai sót khi giải bài tập về đạo hàm, các em cần lưu ý những điều sau:
- Nắm vững các công thức đạo hàm cơ bản.
- Cẩn thận khi áp dụng quy tắc tính đạo hàm.
- Kiểm tra lại kết quả tính đạo hàm.
- Rèn luyện kỹ năng giải bài tập thường xuyên.
Tusach.vn - Đồng hành cùng các em trên con đường học tập
Tusach.vn luôn cập nhật và cung cấp các bài giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách giáo khoa và sách bài tập Toán 11 Kết nối tri thức. Hy vọng rằng, với bài viết này, các em sẽ tự tin hơn trong việc giải bài tập về đạo hàm và đạt kết quả tốt trong môn Toán.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ!
| Công thức đạo hàm | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x2)' = 2x |
| (u + v)' = u' + v' | (x2 + 3x)' = 2x + 3 |