Giải bài 2.29 trang 40 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 2.29 trang 40 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 2.29 trang 40 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, giúp các em học tập tốt hơn.
Các cạnh của hình vuông ban đầu có chiều dài 16cm. Một hình vuông mới được hình thành bằng cách nối các điểm giữa của các cạnh của hình vuông ban đầu và hai trong số các hình tam giác kết quả được tô màu (hình vẽ dưới).
Đề bài
Các cạnh của hình vuông ban đầu có chiều dài 16cm. Một hình vuông mới được hình thành bằng cách nối các điểm giữa của các cạnh của hình vuông ban đầu và hai trong số các hình tam giác kết quả được tô màu (hình vẽ dưới). Nếu quá trình này được lặp lại năm lần nữa, hãy xác định tổng diện tích của vùng được tô màu.
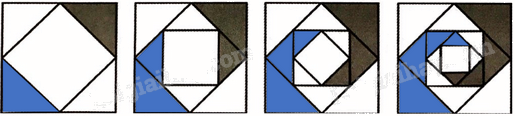
Phương pháp giải - Xem chi tiết
+ Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu là \({u_1}\) và công bội q thì số hạng tổng quát \({u_n}\) của nó được xác định bởi công thức \({u_n} = {u_1}.{q^{n - 1}}\) với \(n \ge 2\)
+ Cho cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q \ne 1\). Đặt \({S_n} = {u_1} + {u_2} + ... + {u_n}\). Khi đó, \({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\)
Lời giải chi tiết
Gọi \({u_n}\) là diện tích hai tam giác được tô màu ở lần thực hiện thứ n. Gọi a là độ dài cạnh của hình vuông ban đầu.
Ở lần 1 thì độ dài cạnh tam giác vuông cân là \(\frac{a}{2}\) nên \({u_1} = 2.\frac{1}{2}.\frac{a}{2}.\frac{a}{2} = \frac{{{a^2}}}{{{2^2}}}\) và độ dài của cạnh hình vuông sau đó là \(\frac{{a\sqrt 2 }}{2}\)
Ở lần 2 thì độ dài cạnh tam giác vuông cân là \(\frac{a}{2}.\frac{{\sqrt 2 }}{2}\) nên \({u_2} = \frac{{{a^2}}}{{{2^3}}}\)
Ở lần 3 thì độ dài cạnh tam giác vuông cân là \(\frac{a}{2}.\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2}\) nên \({u_3} = \frac{{{a^2}}}{{{2^4}}}\)’
Như vậy, dãy số (\({u_n}\)) là cấp số nhân với \({u_1} = \frac{{{a^2}}}{4}\) và công bội \(q = \frac{1}{2}\)
Vậy tổng diện tích sau năm lần thực hiện là \({S_5} = {u_1} = \frac{{1 - {q^5}}}{{1 - q}} = 124\left( {c{m^2}} \right)\)
Giải bài 2.29 trang 40 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 2.29 trang 40 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về Đường thẳng và mặt phẳng trong không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng, cụ thể là xác định mối quan hệ song song, cắt nhau hoặc nằm trong mặt phẳng.
Nội dung bài tập 2.29
Bài tập 2.29 thường bao gồm các dạng câu hỏi sau:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng khi biết phương trình của đường thẳng và mặt phẳng.
- Tìm giao điểm của đường thẳng và mặt phẳng (nếu có).
- Chứng minh một đường thẳng song song với một mặt phẳng.
- Chứng minh một đường thẳng nằm trong một mặt phẳng.
Phương pháp giải bài tập 2.29
Để giải bài tập 2.29 trang 40 SBT Toán 11 Kết nối tri thức hiệu quả, các em cần nắm vững các kiến thức sau:
- Phương trình đường thẳng trong không gian: Dạng tham số và dạng chính tắc.
- Phương trình mặt phẳng trong không gian: Dạng tổng quát.
- Vectơ pháp tuyến của mặt phẳng.
- Vectơ chỉ phương của đường thẳng.
- Điều kiện song song, cắt nhau, nằm trong giữa đường thẳng và mặt phẳng.
Các bước giải bài tập cụ thể:
- Bước 1: Xác định phương trình đường thẳng và mặt phẳng.
- Bước 2: Tìm vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng.
- Bước 3: Kiểm tra mối quan hệ giữa vectơ chỉ phương và vectơ pháp tuyến.
- Bước 4: Kết luận về vị trí tương đối giữa đường thẳng và mặt phẳng.
Ví dụ minh họa (giả định)
Bài toán: Cho đường thẳng (d): x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa đường thẳng (d) và mặt phẳng (P).
Giải:
- Vectơ chỉ phương của đường thẳng (d) là a = (1, -1, 2).
- Vectơ pháp tuyến của mặt phẳng (P) là n = (2, -1, 1).
- Ta có a.n = 1*2 + (-1)*(-1) + 2*1 = 5 ≠ 0.
- Vậy, đường thẳng (d) và mặt phẳng (P) cắt nhau.
Lưu ý quan trọng
Khi giải bài tập về đường thẳng và mặt phẳng, các em cần chú ý:
- Kiểm tra kỹ các điều kiện trước khi kết luận.
- Sử dụng đúng công thức và phương pháp giải.
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
Tusach.vn - Đồng hành cùng các em học Toán
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong sách bài tập Toán 11 Kết nối tri thức. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất trong quá trình học tập!
| Chương | Bài | Trang |
|---|---|---|
| Đường thẳng và mặt phẳng trong không gian | 2.29 | 40 |