Giải bài 1.23 trang 18 SBT Toán 11 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 1.23 trang 18 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
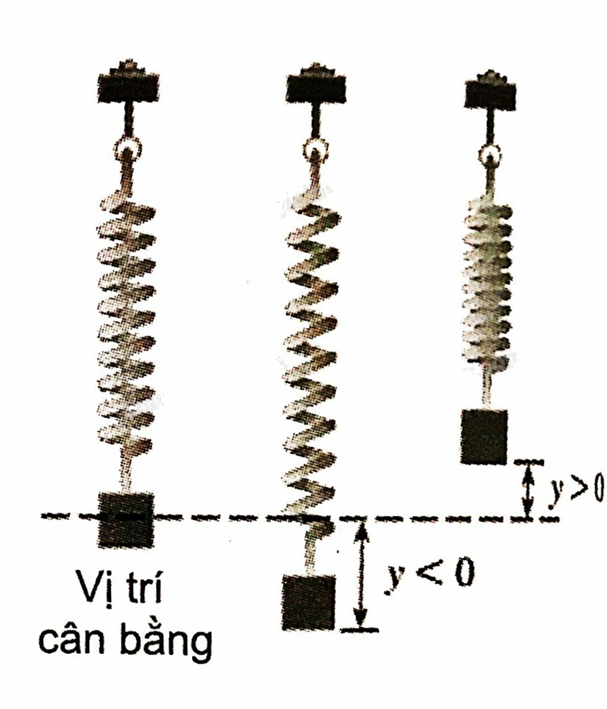
Một con lắc lò xo dạo động điều hòa quanh vị trí cân bằng theo phương trình
ở đó \(y = 25\sin 4\pi t\), y được tính bằng centimet còn thời gian t được tính bằng giây.
Giải bài 1.23 trang 18 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 1.23 trang 18 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng và các điểm đặc biệt của parabol để giải quyết các bài toán liên quan đến ứng dụng thực tế.
Nội dung bài tập 1.23
Bài 1.23 thường bao gồm các dạng bài tập sau:
- Xác định các yếu tố của parabol (a, b, c, đỉnh, trục đối xứng).
- Tìm tập xác định, tập giá trị của hàm số bậc hai.
- Giải các bài toán liên quan đến ứng dụng của parabol trong thực tế (ví dụ: tìm quỹ đạo của vật được ném, tìm giá trị lớn nhất/nhỏ nhất của hàm số).
Lời giải chi tiết bài 1.23 trang 18 SBT Toán 11 - Kết nối tri thức
Để giải bài 1.23 trang 18 SBT Toán 11 Kết nối tri thức, chúng ta cần thực hiện các bước sau:
- Bước 1: Xác định hàm số bậc hai.
- Bước 2: Xác định các hệ số a, b, c.
- Bước 3: Tính tọa độ đỉnh của parabol: xđỉnh = -b/(2a), yđỉnh = -Δ/(4a) (với Δ = b2 - 4ac).
- Bước 4: Xác định trục đối xứng của parabol: x = xđỉnh.
- Bước 5: Xác định các điểm đặc biệt của parabol (giao điểm với trục hoành, trục tung).
- Bước 6: Vận dụng các kiến thức đã học để giải quyết bài toán cụ thể.
Ví dụ minh họa:
Giả sử bài tập yêu cầu tìm tọa độ đỉnh của parabol y = x2 - 4x + 3.
Giải:
- a = 1, b = -4, c = 3
- xđỉnh = -(-4)/(2*1) = 2
- yđỉnh = -( (-4)2 - 4*1*3 )/(4*1) = -(16 - 12)/4 = -1
Vậy tọa độ đỉnh của parabol là (2; -1).
Mẹo giải bài tập hàm số bậc hai
Để giải các bài tập về hàm số bậc hai một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
- Nắm vững các công thức tính tọa độ đỉnh, trục đối xứng, điểm đặc biệt của parabol.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng và chính xác.
- Vẽ đồ thị hàm số để hình dung rõ hơn về tính chất của parabol.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa và sách bài tập, các em có thể tham khảo thêm các tài liệu sau:
- Các trang web học Toán trực tuyến uy tín.
- Các video bài giảng về hàm số bậc hai trên YouTube.
- Các diễn đàn, nhóm học tập Toán trên mạng xã hội.
Kết luận
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã có thể tự tin giải bài 1.23 trang 18 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
