Giải bài 7.6 trang 28 SBT Toán 11 - Kết nối tri thức

Giải bài 7.6 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.6 trang 28 SBT Toán 11 Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 7.6 trang 28 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho các em học sinh.

Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\) vuông tại\(B\).

Đề bài

Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\) vuông tại\(B\). Kẻ \(AM\) vuông góc với \(SB\) tại \(M\) và \(AN\) vuông góc với \(SC\) tại\(N\). Chứng minh rằng:

a)\(BC \bot \left( {SAB} \right)\);

b) \(AM \bot \left( {SBC} \right)\)

c) \(SC \bot \left( {AMN} \right)\)

Phương pháp giải - Xem chi tiết Giải bài 7.6 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Áp dụng định lý sau

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng

một mặt phẳng thì nó vuông góc với mặt phẳng đó.

Chứng minh hai đường thẳng vuông góc dựa vào đường thẳng vuông góc với mặt phẳng

+ \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \subset \alpha \end{array} \right. \Rightarrow a \bot b\)

Lời giải chi tiết

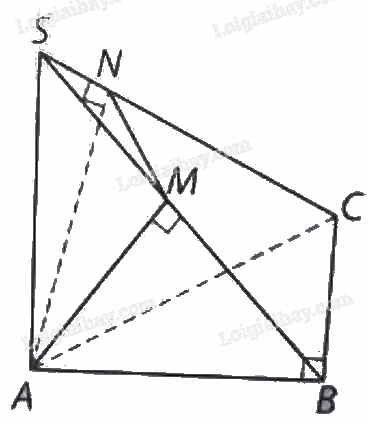
Giải bài 7.6 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

a) Ta có: \(BC \bot AB\)và \(SA \bot \left( {ABC} \right)\) nên\(SA \bot BC\), suy ra \(BC \bot \left( {SAB} \right).\)

b) Vì \(BC \bot \left( {SAB} \right).\) nên \(BC \bot AM.\), mà \(AM \bot SB.\), suy ra \(AM \bot \left( {SBC} \right).\)

c) Vì \(AM \bot \left( {SBC} \right).\) nên \(AM \bot SC.\), mà \(AN \bot SC.\), suy ra \(\left( {AMN} \right) \bot SC.\).

Giải bài 7.6 trang 28 SBT Toán 11 Kết nối tri thức: Tổng quan

Bài 7.6 trang 28 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về phép biến hình. Bài tập này yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán thực tế. Việc nắm vững các tính chất và công thức liên quan đến các phép biến hình là rất quan trọng để hoàn thành tốt bài tập này.

Nội dung bài tập 7.6 trang 28 SBT Toán 11 Kết nối tri thức

Bài tập 7.6 thường bao gồm các dạng bài sau:

Xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép biến hình cho trước.
Tìm tâm, trục hoặc góc của phép biến hình.
Chứng minh một hình là ảnh của một hình khác qua một phép biến hình.
Ứng dụng các phép biến hình vào việc giải quyết các bài toán hình học.

Lời giải chi tiết bài 7.6 trang 28 SBT Toán 11 Kết nối tri thức

Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Ở đây sẽ là lời giải chi tiết của bài tập 7.6, ví dụ):

Ví dụ: Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm ảnh A' của điểm A qua phép tịnh tiến đó.

Giải:

Áp dụng công thức phép tịnh tiến: A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)

Thay số: A'(1 + 3; 2 - 1) = A'(4; 1)

Vậy, ảnh A' của điểm A qua phép tịnh tiến theo vectơ v là A'(4; 1).

Phương pháp giải bài tập về phép biến hình

Để giải tốt các bài tập về phép biến hình, các em cần:

Nắm vững định nghĩa và tính chất của từng phép biến hình (phép tịnh tiến, phép quay, phép đối xứng trục, phép đối xứng tâm).
Hiểu rõ công thức biến đổi tọa độ của các điểm, đường thẳng và hình qua từng phép biến hình.
Luyện tập thường xuyên với các bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải bài tập.
Vẽ hình minh họa để dễ dàng hình dung và tìm ra lời giải.

Mẹo giải nhanh bài tập phép biến hình

Một số mẹo nhỏ có thể giúp các em giải nhanh bài tập:

Sử dụng các công thức biến đổi tọa độ một cách linh hoạt.
Chú ý đến các tính chất đặc biệt của từng phép biến hình.
Kết hợp các phép biến hình để giải quyết các bài toán phức tạp.

Tài liệu tham khảo thêm

Để học tốt hơn về phép biến hình, các em có thể tham khảo thêm:

Sách giáo khoa Toán 11
Sách bài tập Toán 11
Các trang web học toán trực tuyến uy tín

Kết luận

Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh đã có thể tự tin giải bài 7.6 trang 28 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao!