Giải bài 4.26 trang 63 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.26 trang 63 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu đến các em lời giải chi tiết bài 4.26 trang 63 sách bài tập Toán 11 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm.
Chúng tôi sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Gọi E là một điểm bất kì thuộc cạnh SA
Đề bài
Cho hình chóp S.ABCD có đáy là hình thang (AB//CD). Gọi E là một điểm bất kì thuộc cạnh SA. Gọi (P) là mặt phẳng qua E và song song với hai đường thẳng AB và SC.
a) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (SAC), từ đó tìm một điểm chung của mặt phẳng (P) và mặt phẳng (ABCD).
b) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (ABCD).
c) Xác định giao tuyến của mặt phẳng (P) và các mặt còn lại của hình chóp.
Phương pháp giải - Xem chi tiết
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a song song với b.
Lời giải chi tiết
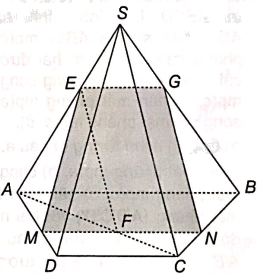
a) Mặt phẳng (SAC) chứa đường thẳng SC song song với mặt phẳng (P) nên giao tuyến của hai mặt phẳng (SAC) và (P) song song với SC. Do đó, trong mặt phẳng (SAC), vẽ đường thẳng EF//SC (F thuộc AC) thì EF là giao tuyến của hai mặt phẳng (P) và (SAC). Điểm F là điểm chung của mặt phẳng (P) và mặt phẳng (ABCD).
b) Trong mặt phẳng (ABCD), vẽ đường thẳng MN qua F song song với AB \(\left( {M \in AD,N \in BC} \right)\) thì MN là giao tuyến của (P) và mặt phẳng (ABCD)
c) Trong mặt phẳng (SAB), vẽ đường thẳng EG//AB (G thuộc SB) thì EG là giao tuyến của hai mặt phẳng (P) và (SAB). Các giao tuyến của (P) và các mặt của hình chóp là EG, MN, EM, GN.
Giải bài 4.26 trang 63 SBT Toán 11 - Kết nối tri thức: Hướng dẫn chi tiết
Bài 4.26 trang 63 sách bài tập Toán 11 Kết nối tri thức yêu cầu chúng ta tìm đạo hàm của hàm số và sử dụng đạo hàm để giải quyết các bài toán liên quan đến tính đơn điệu của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
- Định nghĩa đạo hàm: Đạo hàm của hàm số f(x) tại điểm x được ký hiệu là f'(x) và biểu thị tốc độ thay đổi tức thời của hàm số tại điểm đó.
- Các quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp, và các hàm số cơ bản (hàm số mũ, hàm số logarit, hàm lượng giác).
- Ứng dụng của đạo hàm: Sử dụng đạo hàm để xét tính đơn điệu của hàm số, tìm cực trị của hàm số, và giải các bài toán tối ưu.
Lời giải chi tiết bài 4.26 trang 63 SBT Toán 11 - Kết nối tri thức
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích từng bước:
Phần 1: Tính đạo hàm của hàm số
Trước tiên, chúng ta cần tính đạo hàm của hàm số đã cho. Sử dụng các quy tắc tính đạo hàm đã học, ta thực hiện các phép biến đổi để tìm ra đạo hàm f'(x).
Phần 2: Xét dấu đạo hàm và kết luận về tính đơn điệu
Sau khi tính được đạo hàm f'(x), chúng ta cần xét dấu của đạo hàm trên các khoảng xác định của hàm số. Dựa vào dấu của đạo hàm, ta có thể kết luận về tính đơn điệu của hàm số:
- Nếu f'(x) > 0 trên một khoảng nào đó, hàm số f(x) đồng biến trên khoảng đó.
- Nếu f'(x) < 0 trên một khoảng nào đó, hàm số f(x) nghịch biến trên khoảng đó.
Phần 3: Giải các bài toán liên quan (nếu có)
Nếu bài tập yêu cầu giải các bài toán liên quan đến tính đơn điệu của hàm số, chúng ta sử dụng kết quả đã tìm được ở phần 2 để giải quyết các bài toán đó.
Ví dụ minh họa
Giả sử hàm số f(x) = x3 - 3x2 + 2. Ta có:
- f'(x) = 3x2 - 6x
- Xét dấu f'(x): f'(x) = 0 khi x = 0 hoặc x = 2.
- Bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Vậy hàm số f(x) đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).
Lưu ý khi giải bài tập
- Luôn kiểm tra kỹ các quy tắc tính đạo hàm trước khi áp dụng.
- Chú ý xét dấu đạo hàm trên các khoảng xác định của hàm số.
- Sử dụng các kiến thức về tính đơn điệu của hàm số để giải quyết các bài toán liên quan.
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin giải bài 4.26 trang 63 sách bài tập Toán 11 Kết nối tri thức một cách hiệu quả. Chúc các em học tốt!