Giải bài 4.35 trang 68 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.35 trang 68 SBT Toán 11 Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 4.35 trang 68 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, hỗ trợ tối đa cho quá trình học tập của các em.
Cho hình hộp ABCD.A’B’C’D’.
Đề bài
Cho hình hộp ABCD.A’B’C’D’.
a) Xác định giao tuyến d của hai mặt phẳng (ADC’B’) và (A’D’CB).
b) Chứng minh rằng d // AD.
c) Chứng minh rằng d đi qua trung điểm của các đường chéo của hình hộp.
Phương pháp giải - Xem chi tiết
Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó.
Lời giải chi tiết
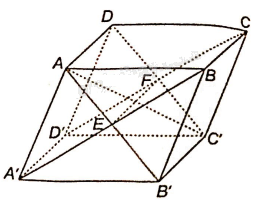
a) Gọi E là giao điểm của AB’ và A’B; gọi F là giao điểm của CD’ và C’D. Vì đường thẳng EF vừa thuộc cả hai mặt phẳng (ADC’B’) và (A’D’CB) nên EF là giao tuyến của hai mặt phẳng (ADC’B’) và (A’D’CB).
b) Hai mặt phẳng (ADC’B’) và (A’D’CB) chứa hai đường thẳng song song là AD và BC nên giao tuyến EF của hai mặt phẳng đó song song với AD.
c) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, \(AD = BC\) và BC//B’C’ và \(BC = B'C'\), do đó ADC’B’ là hình bình hành.
Vì E, F lần lượt là trung điểm của AB’ và CD’ nên EF đi qua trung điểm của AC’. Vì các đường chéo của hình hộp cùng đi qua trung điểm của mỗi đường nên đường thẳng EF đi qua trung điểm các đường chéo đó.
Giải bài 4.35 trang 68 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp
Bài 4.35 trang 68 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác để giải quyết các bài toán thực tế.
Nội dung bài tập 4.35 trang 68 SBT Toán 11 Kết nối tri thức
Thông thường, bài 4.35 sẽ đưa ra một tình huống cụ thể liên quan đến sự thay đổi của một đại lượng nào đó. Ví dụ, bài toán có thể mô tả một vật thể chuyển động và yêu cầu tính vận tốc hoặc gia tốc của vật tại một thời điểm nhất định. Hoặc bài toán có thể liên quan đến việc tối ưu hóa một hàm số nào đó, chẳng hạn như tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số.
Phương pháp giải bài tập 4.35 trang 68 SBT Toán 11 Kết nối tri thức
- Xác định hàm số: Bước đầu tiên là xác định hàm số mô tả mối quan hệ giữa các đại lượng trong bài toán.
- Tính đạo hàm: Tiếp theo, tính đạo hàm của hàm số vừa xác định.
- Giải phương trình: Sử dụng đạo hàm để giải các phương trình liên quan đến bài toán, chẳng hạn như phương trình tìm điểm cực trị hoặc phương trình tìm vận tốc, gia tốc.
- Kiểm tra kết quả: Cuối cùng, kiểm tra kết quả để đảm bảo rằng nó phù hợp với điều kiện của bài toán.
Ví dụ minh họa giải bài 4.35 trang 68 SBT Toán 11 Kết nối tri thức
Bài toán: Một vật thể chuyển động theo phương trình s(t) = t3 - 6t2 + 9t + 2, trong đó s(t) là quãng đường đi được của vật tại thời điểm t (t tính bằng giây, s tính bằng mét). Tính vận tốc của vật tại thời điểm t = 2 giây.
Lời giải
1. Tính vận tốc: Vận tốc của vật tại thời điểm t là đạo hàm của quãng đường đi được theo thời gian, tức là v(t) = s'(t).
2. Tính đạo hàm: s'(t) = 3t2 - 12t + 9.
3. Tính vận tốc tại t = 2: v(2) = 3(2)2 - 12(2) + 9 = 12 - 24 + 9 = -3 (m/s).
Kết luận: Vận tốc của vật tại thời điểm t = 2 giây là -3 m/s.
Các dạng bài tập thường gặp trong bài 4.35 trang 68 SBT Toán 11 Kết nối tri thức
- Bài toán về tối ưu hóa: Tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số.
- Bài toán về chuyển động: Tính vận tốc, gia tốc của một vật thể.
- Bài toán về tốc độ thay đổi: Tính tốc độ thay đổi của một đại lượng nào đó.
Lưu ý khi giải bài tập 4.35 trang 68 SBT Toán 11 Kết nối tri thức
Để giải quyết hiệu quả các bài tập trong bài 4.35, các em cần nắm vững các kiến thức về:
- Đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Quy tắc tính đạo hàm của hàm hợp.
- Ứng dụng của đạo hàm trong việc giải các bài toán thực tế.
Tusach.vn hy vọng với bài giải chi tiết này, các em sẽ hiểu rõ hơn về cách giải bài 4.35 trang 68 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!
| Chủ đề | Nội dung |
|---|---|
| Đạo hàm | Công cụ quan trọng để giải quyết các bài toán liên quan đến sự thay đổi. |
| Hàm hợp | Yêu cầu nắm vững quy tắc tính đạo hàm. |
| Ứng dụng | Tối ưu hóa, tính vận tốc, gia tốc,... |