Giải bài 4.38 trang 68 SBT Toán 11 - Kết nối tri thức

Giải bài 4.38 trang 68 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 4.38 trang 68 SBT Toán 11 Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 4.38 trang 68 sách bài tập Toán 11 Kết nối tri thức. Bài học này tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.

Tusach.vn cung cấp đáp án chính xác, phương pháp giải dễ hiểu và lời giải chi tiết, giúp các em hiểu sâu sắc kiến thức và tự tin làm bài tập.

Cho hình hộp ABCD.A’B’C’D’. Gọi O là giao điểm của các đường chéo của hình hộp.

Đề bài

Cho hình hộp ABCD.A’B’C’D’. Gọi O là giao điểm của các đường chéo của hình hộp. Mặt phẳng qua O và song song với mặt phẳng (ABCD) cắt các cạnh AA’, BB’, CC’, DD’ lần lượt tại M, N, P, Q.

a) Chứng minh rằng M, N, P, Q lần lượt là trung điểm của các cạnh AA’, BB’, CC’, DD’.

b) Chứng minh rằng ABCD.MNPQ là hình hộp.

Phương pháp giải - Xem chi tiết Giải bài 4.38 trang 68 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Định lí Thalès: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ

Hình lăng trụ tứ giác ABCD.A’B’C’D’ có hai đáy là hình bình hành được gọi là hình hộp.

Lời giải chi tiết

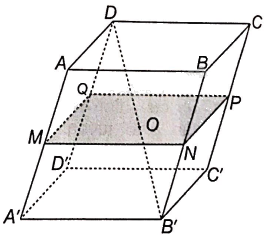
Giải bài 4.38 trang 68 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

a) Áp dụng định lí Thalès cho ba mặt phẳng (ABCD), (MNPQ), (A’B’C’D’) và hai cát tuyến AA’, DB’ ta có: \(\frac{{AM}}{{MA'}} = \frac{{DO}}{{OB'}}\)

Vì O là trung điểm của DB’ nên M là trung điểm của AA’.

Chứng minh tương tự ta có: N, P, Q lần lượt là trung điểm của BB’, CC’, DD’.

b) Vì M, N lần lượt là trung điểm của AA’, BB’ nên MN//AB, \(MN = AB\)

Tương tự ta có: PQ//CD và \(PQ = CD\)

Vì \(AB = CD\) và AB//CD nên \(MN = PQ\) và MN//PQ.

Do đó tứ giác MNPQ là hình bình hành.

Vì các đường thẳng AM, BN, CP, DQ đôi một song song nên suy ra ABCD.MNPQ là hình hộp.

Giải bài 4.38 trang 68 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp

Bài 4.38 trang 68 sách bài tập Toán 11 Kết nối tri thức là một bài toán ứng dụng đạo hàm để giải quyết một vấn đề thực tế. Bài toán thường yêu cầu học sinh tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số trong một khoảng cho trước, hoặc tìm điều kiện để một hàm số thỏa mãn một tính chất nào đó.

Nội dung bài toán 4.38 trang 68 SBT Toán 11 Kết nối tri thức

Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức sau:

Đạo hàm: Khái niệm đạo hàm, quy tắc tính đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
Ứng dụng đạo hàm: Tìm cực trị của hàm số, khảo sát hàm số, giải phương trình, bất phương trình.
Kỹ năng giải toán: Phân tích bài toán, xây dựng mô hình toán học, sử dụng các công cụ đạo hàm để giải quyết bài toán.

Lời giải chi tiết bài 4.38 trang 68 SBT Toán 11 Kết nối tri thức

(Ở đây sẽ là lời giải chi tiết của bài toán 4.38. Vì không có nội dung cụ thể của bài toán, nên phần này sẽ được mô tả chung.)

Để giải bài toán, ta thực hiện các bước sau:

Xác định hàm số: Xác định hàm số cần tìm cực trị hoặc khảo sát.
Tính đạo hàm: Tính đạo hàm cấp nhất của hàm số.
Tìm điểm dừng: Giải phương trình đạo hàm cấp nhất bằng 0 để tìm các điểm dừng.
Khảo sát dấu đạo hàm: Khảo sát dấu đạo hàm cấp nhất trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến của hàm số.
Tìm cực trị: Xác định các điểm cực đại, cực tiểu của hàm số.
Kết luận: Dựa vào kết quả khảo sát để trả lời câu hỏi của bài toán.

Ví dụ minh họa (giả định)

Giả sử bài toán yêu cầu tìm giá trị lớn nhất của hàm số f(x) = -x² + 4x + 1 trên đoạn [0; 3].

Ta thực hiện như sau:

f'(x) = -2x + 4
Giải f'(x) = 0, ta được x = 2
Khảo sát dấu f'(x):

x < 2: f'(x) > 0 (hàm số đồng biến)
x > 2: f'(x) < 0 (hàm số nghịch biến)

Vậy hàm số đạt cực đại tại x = 2.
f(2) = -2² + 4*2 + 1 = 5
Kiểm tra giá trị tại các đầu mút của đoạn [0; 3]:

f(0) = 1
f(3) = -3² + 4*3 + 1 = 4

Vậy giá trị lớn nhất của hàm số trên đoạn [0; 3] là 5, đạt được tại x = 2.

Lưu ý khi giải bài tập ứng dụng đạo hàm

Đọc kỹ đề bài để hiểu rõ yêu cầu của bài toán.
Xác định đúng hàm số cần khảo sát hoặc tìm cực trị.
Sử dụng đúng các quy tắc tính đạo hàm.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Tusach.vn – Đồng hành cùng bạn học Toán 11

Tusach.vn luôn đồng hành cùng các em học sinh trong quá trình học tập môn Toán 11. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và phương pháp giải bài tập hiệu quả. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!