Giải bài 4.4 trang 55 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.4 trang 55 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Bài viết này của tusach.vn sẽ cung cấp lời giải chi tiết và dễ hiểu bài 4.4 trang 55 sách bài tập Toán 11 Kết nối tri thức. Chúng tôi sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Mục tiêu của chúng tôi là hỗ trợ các em học tập hiệu quả và đạt kết quả tốt nhất trong môn Toán.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD.
Đề bài
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi P là một điểm thuộc cạnh BC sao cho PC = 2PB.
a) Xác định giao điểm của đường thẳng BD và mặt phẳng (MNP).
b) Xác định giao điểm của đường thẳng AC và mặt phẳng (MNP).
c) Xác định giao điểm của đường thẳng AD và mặt phẳng (MNP).
Phương pháp giải - Xem chi tiết
Để xác định giao điểm của đường thẳng d và mặt phẳng (P), ta tìm một đường thẳng trong mặt phẳng (P) sao cho đường thẳng đó đồng phẳng với d. Xác giao điểm của đường thẳng đó với d. Giao điểm ấy chính là giao điểm giữa đường thẳng d và mặt phẳng (P).
Lời giải chi tiết
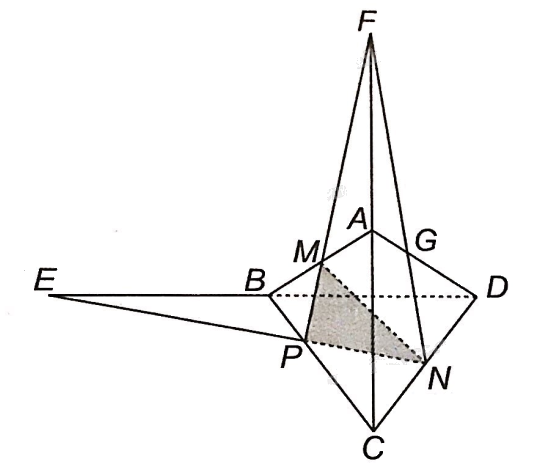
a) Trong mặt phẳng (BCD): Gọi E là giao điểm của BD và PN.
Vậy giao điểm của đường thẳng BD và mặt phẳng (MNP) là điểm E.
b) Trong mặt phẳng (ABC): gọi F là giao điểm của AC và MP.
Vậy giao điểm của đường thẳng AC và mặt phẳng (MNP) là điểm F.
c) Trong mặt phẳng (ADC): gọi G là giao điểm của AD và NF.
Vậy giao điểm của đường thẳng AD và mặt phẳng (MNP) là điểm G.
Giải bài 4.4 trang 55 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp
Bài 4.4 trang 55 sách bài tập Toán 11 Kết nối tri thức thường xoay quanh các chủ đề về hàm số lượng giác, đặc biệt là các phép biến đổi lượng giác và ứng dụng của chúng trong việc giải phương trình lượng giác. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản sau:
- Các công thức lượng giác cơ bản: sin2x + cos2x = 1, tanx = sinx/cosx, cotx = cosx/sinx, ...
- Các phép biến đổi lượng giác: Công thức cộng, trừ, nhân, chia góc, công thức hạ bậc, nâng bậc, ...
- Phương pháp giải phương trình lượng giác: Sử dụng các công thức lượng giác để đưa phương trình về dạng cơ bản, sau đó giải tìm nghiệm.
Giải chi tiết bài 4.4 trang 55 SBT Toán 11 - Kết nối tri thức
Để cung cấp lời giải chi tiết, chúng ta cần biết nội dung cụ thể của bài 4.4. Tuy nhiên, dưới đây là một ví dụ minh họa cách tiếp cận và giải quyết một bài tập tương tự:
Ví dụ minh họa:
Giả sử bài 4.4 yêu cầu giải phương trình: 2sin2x - 3sinx + 1 = 0
- Đặt ẩn phụ: Đặt t = sinx, phương trình trở thành: 2t2 - 3t + 1 = 0
- Giải phương trình bậc hai: Giải phương trình trên, ta được t = 1 hoặc t = 1/2
- Tìm nghiệm x:
- Nếu t = 1, thì sinx = 1 => x = π/2 + kπ, k ∈ Z
- Nếu t = 1/2, thì sinx = 1/2 => x = π/6 + kπ hoặc x = 5π/6 + kπ, k ∈ Z
Lưu ý khi giải bài tập
Khi giải các bài tập về hàm số lượng giác, cần chú ý những điều sau:
- Kiểm tra điều kiện: Đảm bảo rằng các giá trị của x thỏa mãn điều kiện của phương trình (ví dụ: mẫu số khác 0, logarit có cơ số lớn hơn 0 và khác 1, ...).
- Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp tính toán nhanh chóng và chính xác các giá trị lượng giác.
- Luyện tập thường xuyên: Luyện tập nhiều bài tập khác nhau sẽ giúp các em nắm vững kiến thức và kỹ năng giải bài tập.
Tusach.vn - Hỗ trợ học tập Toán 11 hiệu quả
Tusach.vn là website cung cấp lời giải chi tiết và chính xác các bài tập trong sách giáo khoa và sách bài tập Toán 11 Kết nối tri thức. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các phương pháp giải bài tập hiệu quả nhất. Hãy truy cập tusach.vn để được hỗ trợ học tập tốt nhất!
Bảng tổng hợp công thức lượng giác thường dùng
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
| sin(a + b) = sin a cos b + cos a sin b | Công thức cộng góc sin |
| cos(a + b) = cos a cos b - sin a sin b | Công thức cộng góc cos |
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về cách giải bài 4.4 trang 55 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!