Logo

Giải bài 7.52 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Tổng quan nội dung

Giải bài 7.52 trang 43 SBT Toán 11 Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 7.52 trang 43 sách bài tập Toán 11 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.

Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) biết ABCD là hình vuông cạnh bằng a và \(SA = a\sqrt 2 \)

Đề bài

Cho hình chóp S.ABCD có \(SA \bot (ABCD)\) biết ABCD là hình vuông cạnh bằng a và \(SA = a\sqrt 2 \)

a) Chứng minh rằng\((SAC) \bot (SBD)\) và \((SAD) \bot (SCD)\)

b) Gọi BE, DF là hai đường cao của tam giác SBD. Chứng minh \((ACF) \bot (SBC)\) và \((AEF) \bot (SAC)\)

c) Tính theo a khoản cách giữa hai đường thẳng BD và SC

Phương pháp giải - Xem chi tiếtGiải bài 7.52 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

a) Chứng minh \(BD \bot \left( {SAC} \right)\) từ đó suy ra \(\left( {SBD} \right) \bot \left( {SAC} \right)\).

b) Chứng minh \(AF \bot \left( {SBC} \right)\) từ đó suy ra \(\left( {ACF} \right) \bot \left( {SBC} \right)\).

Chứng minh \(SC \bot \left( {AEF} \right)\) suy ra \(\left( {AEF} \right) \bot \left( {SAC} \right)\).

c) Dựng đoạn vuông góc chung của \(BD\) và \(SC\),

Tính độ dài đoạn vuông góc chung của \(BD\) và \(SC\),

Lời giải chi tiết

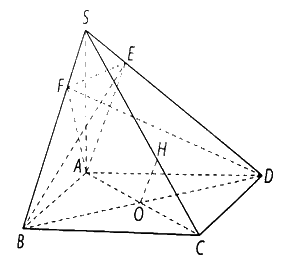
Giải bài 7.52 trang 43 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

a) Ta có: \(BD \bot AC,SA \bot \left( {ABCD} \right)\) nên \(SA \bot BD\), suy ra \(BD \bot \left( {SAC} \right)\), mà mặt phẳng \(\left( {SBD} \right)\) chứa đường thẳng \(BD\), do đó \(\left( {SBD} \right) \bot \left( {SAC} \right)\).

Ta có: \(CD \bot AD,CD \bot SA\), suy ra \(CD \bot \left( {SAD} \right)\), mà mặt phẳng \(\left( {SCD} \right)\) chứa đường thẳng \(CD\), do đó \(\left( {SCD} \right) \bot \left( {SAD} \right)\).

b) Ta có: \(AD \bot \left( {SAB} \right)\) nên \(AD \bot SB\), mà \(SB \bot DF\) suy ra \(SB \bot \left( {ADF} \right)\), do đó

\(SB \bot AF\).

Ta lại có \(BC \bot \left( {SAB} \right)\) nên \(BC \bot AF\), suy ra \(AF \bot \left( {SBC} \right)\), mà mặt phẳng \(\left( {ACF} \right)\) chứa đường thẳng \(AF\) nên \(\left( {ACF} \right) \bot \left( {SBC} \right)\).

Vì \(AF \bot \left( {SBC} \right)\) nên \(AF \bot SC\).

 Tương tự, ta có \(AE \bot \left( {SCD} \right)\) nên \(AE \bot SC\), suy ra \(SC \bot \left( {AEF} \right)\), mà mặt phẳng \(\left( {SAC} \right)\) chứa đường thẳng \(SC\) nên \(\left( {AEF} \right) \bot \left( {SAC} \right)\).

c) Gọi \(O\) là giao điểm của \(AC\) và \(BD\), kẻ \(OH \bot SC\) tại \(H\), mà \(BD \bot \left( {SAC} \right)\) nên \(OH \bot BD\), suy ra \(OH\) là đoạn vuông góc chung của \(BD\) và \(SC\), hay \(d\left( {BD,SC} \right) = OH\)

Ta có: \(\Delta CHO\) đồng dạng với \(\Delta CAS\) nên \(\frac{{OC}}{{CS}} = \frac{{OH}}{{AS}}\), suy ra \(OH = \frac{{AS \cdot OC}}{{CS}} = \frac{a}{2}\).

Vậy \(d\left( {BD,SC} \right) = \frac{a}{2}\).

Giải bài 7.52 trang 43 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp

Bài 7.52 trang 43 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm và công thức sau:

  • Đạo hàm: Định nghĩa, ý nghĩa hình học và vật lý của đạo hàm.
  • Quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
  • Cực trị của hàm số: Điều kiện cần và đủ để hàm số đạt cực trị.
  • Ứng dụng của đạo hàm: Tìm cực trị, khảo sát hàm số, giải các bài toán tối ưu.

Nội dung bài tập 7.52 trang 43 SBT Toán 11 Kết nối tri thức

Bài tập 7.52 thường yêu cầu học sinh thực hiện các công việc sau:

  1. Tìm đạo hàm của hàm số đã cho.
  2. Giải phương trình đạo hàm bằng 0 để tìm các điểm cực trị.
  3. Xác định loại cực trị (cực đại hoặc cực tiểu) bằng cách sử dụng dấu của đạo hàm cấp hai hoặc phương pháp xét dấu đạo hàm.
  4. Tính giá trị của hàm số tại các điểm cực trị.

Lời giải chi tiết bài 7.52 trang 43 SBT Toán 11 Kết nối tri thức

Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu tìm cực trị của hàm số f(x) = x3 - 3x2 + 2.

Bước 1: Tìm đạo hàm f'(x)

f'(x) = 3x2 - 6x

Bước 2: Giải phương trình f'(x) = 0

3x2 - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2

Bước 3: Xác định loại cực trị

Ta tính đạo hàm cấp hai: f''(x) = 6x - 6

f''(0) = -6 < 0, vậy x = 0 là điểm cực đại.

f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu.

Bước 4: Tính giá trị của hàm số tại các điểm cực trị

f(0) = 2

f(2) = 8 - 12 + 2 = -2

Vậy, hàm số f(x) đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.

Mẹo giải bài tập 7.52 trang 43 SBT Toán 11 Kết nối tri thức

  • Nắm vững các công thức tính đạo hàm.
  • Sử dụng đạo hàm cấp hai hoặc phương pháp xét dấu đạo hàm để xác định loại cực trị.
  • Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.
  • Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.

Tusach.vn – Nơi đồng hành cùng bạn học Toán 11

Tusach.vn tự hào là một trong những trang web cung cấp lời giải bài tập Toán 11 uy tín và chất lượng nhất. Chúng tôi luôn cập nhật những lời giải mới nhất, chính xác nhất và dễ hiểu nhất để giúp các em học tập tốt hơn. Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!

Chủ đềLiên kết
Giải bài tập Toán 11 Kết nối tri thứchttps://tusach.vn/toan-11-ket-noi-tri-thuc
Đạo hàm và ứng dụnghttps://tusach.vn/dao-ham-va-ung-dung