Giải bài 1.21 trang 18 Sách bài tập Toán 11 - Kết nối tri thức

Giải bài 1.21 trang 18 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 1.21 trang 18 SBT Toán 11 Kết nối tri thức

Bài 1.21 trang 18 Sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Từ đồ thị hàm số \(y = \cos {\rm{ }}x\), hãy vẽ các đồ thị hàm số sau:

Đề bài

Từ đồ thị hàm số \(y = \cos {\rm{ }}x\), hãy vẽ các đồ thị hàm số sau:

a) \(y = \, - \cos {\rm{ }}x\);

b) \(y = \,|\cos {\rm{ }}x|\);

c) \(y = \cos {\rm{ }}x + 1\);

d) \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\).

Phương pháp giải - Xem chi tiết Giải bài 1.21 trang 18 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Từ đồ thị \(y = \cos {\rm{ }}x\), ta linh hoạt dịch chuyển đồ thị theo yêu cầu đề bài. Vẽ đồ thị \(y = \cos {\rm{ }}x\) bằng nét đứt và vẽ đồ thị trong đề bài bằng nét liền.

Lời giải chi tiết

a) Lấy đối xứng đồ thị hàm số \(y = \cos {\rm{ }}x\) qua trục hoành, ta được đồ thị hàm số \(y = \, - \cos {\rm{ }}x\).

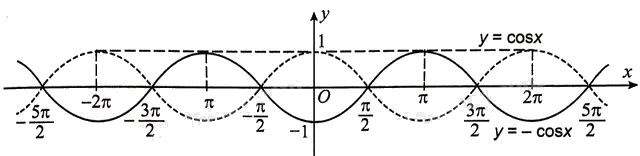
Giải bài 1.21 trang 18 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

Trong hình trên, đồ thị hàm số \(y = \cos {\rm{ }}x\) là đường nét đứt còn đồ thị hàm số \(y = \, - \cos {\rm{ }}x\) là đường nét liền.

b) Ta có

\(y = \,|\cos {\rm{ }}x|\, = \left\{ \begin{array}{l}\cos x\,\,\,\,\,\,{\rm{khi}}\,\,\,\cos x \ge 0\\ - \cos x\,\,{\rm{khi}}\,\,\,\cos x < 0\end{array} \right.\)

Từ đó, để vẽ đồ thị hàm số \(y = \,|\cos {\rm{ }}x|\) ta vẽ đồ thị hàm số \(y = \cos {\rm{ }}x\) ở phía trên trục Ox và lấy đối xứng qua trục Ox phần đồ thị hàm số \(y = \cos {\rm{ }}x\) ở phía dưới trục Ox. Trong hình trên, đồ thị hàm số \(y = \cos {\rm{ }}x\) là đường nét đứt còn đồ thị hàm số \(y = \,|\cos {\rm{ }}x|\) là đường nét liền.

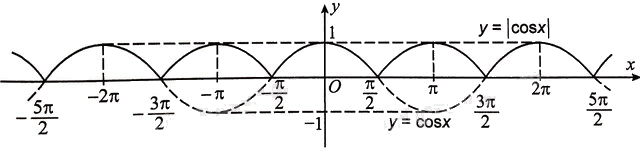
Giải bài 1.21 trang 18 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 3

c) Để vẽ hàm số \(y = \cos {\rm{ }}x + 1\) đầu tiên ta vẽ hàm số \(y = \cos {\rm{ }}x\), sau đó dịch chuyển đồ thị này dọc theo trục Oy lên phía trên 1 đơn vị, ta được đồ thị hàm số. Trong hình dưới đây, đồ thị hàm số \(y = \cos {\rm{ }}x + 1\) là đường nét liền.

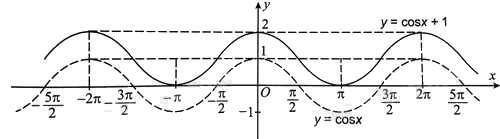
Giải bài 1.21 trang 18 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 4

d) Để vẽ hàm số \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\) đầu tiên ta vẽ hàm số \(y = \cos {\rm{ }}x\), sau đó dịch chuyển đồ thị này dọc theo trục Ox sang bên trái \(\frac{\pi }{2}\) đơn vị, ta được đồ thị hàm số. Trong hình dưới đây, đồ thị hàm số \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\) là đường nét liền.

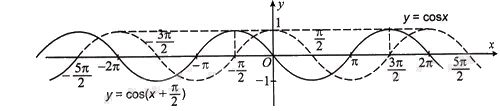
Giải bài 1.21 trang 18 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 5

Giải bài 1.21 trang 18 SBT Toán 11 Kết nối tri thức: Chi tiết và Dễ hiểu

Bài 1.21 trang 18 Sách bài tập Toán 11 Kết nối tri thức yêu cầu chúng ta tìm số hạng tổng quát của dãy số và sử dụng các công thức về cấp số cộng, cấp số nhân để giải quyết. Dưới đây là lời giải chi tiết, từng bước, giúp bạn hiểu rõ cách tiếp cận và áp dụng kiến thức đã học.

Đề bài:

Cho dãy số (u_n) xác định bởi:

u₁ = 5
u_n+1 = u_n + 3

a) Tìm số hạng tổng quát u_n của dãy số.

b) Số 50 có là số hạng của dãy số không? Nếu có, thì nó là số hạng thứ mấy?

Lời giải:

a) Tìm số hạng tổng quát u_n:

Ta có: u₂ = u₁ + 3 = 5 + 3 = 8

u₃ = u₂ + 3 = 8 + 3 = 11

u₄ = u₃ + 3 = 11 + 3 = 14

Nhận thấy sự khác biệt giữa các số hạng liên tiếp là một hằng số, d = 3. Do đó, dãy số (u_n) là một cấp số cộng với số hạng đầu u₁ = 5 và công sai d = 3.

Số hạng tổng quát của cấp số cộng được tính theo công thức: u_n = u₁ + (n - 1)d

Thay u₁ = 5 và d = 3 vào công thức, ta được:

u_n = 5 + (n - 1)3 = 5 + 3n - 3 = 3n + 2

Vậy, số hạng tổng quát của dãy số là u_n = 3n + 2.

b) Kiểm tra xem 50 có là số hạng của dãy số không:

Để kiểm tra xem 50 có là số hạng của dãy số không, ta giải phương trình:

u_n = 50

3n + 2 = 50

3n = 48

n = 16

Vì n = 16 là một số nguyên dương, nên 50 là số hạng thứ 16 của dãy số.

Kết luận:

a) Số hạng tổng quát của dãy số là u_n = 3n + 2.

b) Số 50 là số hạng thứ 16 của dãy số.

Mở rộng và Lưu ý:

Bài tập này giúp củng cố kiến thức về cấp số cộng và cách tìm số hạng tổng quát. Khi gặp các bài toán tương tự, bạn cần xác định xem dãy số có phải là cấp số cộng hay không bằng cách kiểm tra sự khác biệt giữa các số hạng liên tiếp. Nếu là cấp số cộng, hãy sử dụng công thức u_n = u₁ + (n - 1)d để tìm số hạng tổng quát.

Ngoài ra, hãy chú ý đến điều kiện của n (n là số nguyên dương) để xác định xem một số có phải là số hạng của dãy số hay không.

Tusach.vn hy vọng với lời giải chi tiết này, bạn đã hiểu rõ cách giải bài 1.21 trang 18 SBT Toán 11 Kết nối tri thức. Chúc bạn học tốt!