Giải bài 4.61 trang 74 SBT Toán 11 - Kết nối tri thức

Giải bài 4.61 trang 74 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 4.61 trang 74 SBT Toán 11 Kết nối tri thức

Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 4.61 trang 74 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.

Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, hỗ trợ tối đa cho quá trình học tập của các em.

Cho hình lăng trụ tứ giác ABCD.A’B’C’D’

Đề bài

Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Gọi M, N, M’, N’ lần lượt là trung điểm của các cạnh AB, CD, A’B’, C’D’.

a) Chứng minh rằng bốn điểm M, N, M’, N’ đồng phẳng và tứ giác MNN’M’ là hình bình hành

b) Giả sử MN không song song với BC. Xác định giao tuyến của hai mặt phẳng (MNN’M’) và (BCC’B’).

Phương pháp giải - Xem chi tiết Giải bài 4.61 trang 74 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

+ Để chứng minh bốn điểm M, N, M’, N’ đồng phẳng ta có thể chứng minh hai đường thẳng MM’//NN’.

+ Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành.

+ Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Lời giải chi tiết

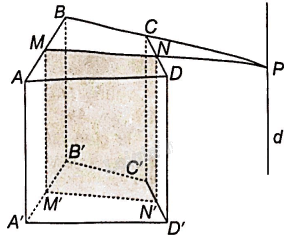
Giải bài 4.61 trang 74 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

a) Vì M, M’ lần lượt là trung điểm của AB, A’B’ của hình bình hành ABB’A’ nên MM’//AA’ và \(MM' = AA'\)

Tương tự ta có: NN’//DD’ và \(NN' = DD'\)

Tứ giác ADD’A’ là hình bình hành nên AA’//DD’ và \(AA' = DD'\).

Do đó, \(MM' = NN'\) và MM’//NN’, suy ra bốn điểm M, N, M’, N’ đồng phẳng và tứ giác MNN’M’ là hình bình hành.

b) Trong mặt phẳng (ABCD), gọi P là giao điểm của hai đường thẳng MN và BC.

Vì BB’// MM’ nên giao tuyến của hai mặt phẳng (MNN’M’) và (BCC’B’) là đường thẳng d qua P và song song với BB’.

Giải bài 4.61 trang 74 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp

Bài 4.61 trang 74 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác để giải quyết các bài toán thực tế.

Nội dung bài tập 4.61

Thông thường, bài 4.61 sẽ đưa ra một tình huống thực tế liên quan đến sự thay đổi của một đại lượng nào đó. Ví dụ, bài toán có thể mô tả sự thay đổi vận tốc của một vật thể, sự thay đổi nhiệt độ theo thời gian, hoặc sự thay đổi sản lượng của một nhà máy. Học sinh cần sử dụng đạo hàm để tìm ra tốc độ thay đổi của đại lượng đó tại một thời điểm cụ thể.

Phương pháp giải bài tập 4.61

Xác định hàm số: Bước đầu tiên là xác định hàm số mô tả mối quan hệ giữa các đại lượng trong bài toán.
Tính đạo hàm: Tiếp theo, tính đạo hàm của hàm số vừa xác định.
Thay giá trị: Cuối cùng, thay giá trị của biến độc lập vào đạo hàm để tìm ra tốc độ thay đổi của đại lượng cần tìm.

Giải chi tiết bài 4.61 trang 74 SBT Toán 11 Kết nối tri thức

Để minh họa phương pháp giải, chúng ta cùng xem xét một ví dụ cụ thể:

Ví dụ: Một vật thể chuyển động theo phương trình s(t) = t³ - 6t² + 9t + 2, trong đó s(t) là quãng đường vật thể đi được sau thời gian t (giây). Tính vận tốc của vật thể tại thời điểm t = 2 giây.

Giải:

Hàm vận tốc: Vận tốc của vật thể là đạo hàm của quãng đường theo thời gian: v(t) = s'(t) = 3t² - 12t + 9
Vận tốc tại t = 2: Thay t = 2 vào hàm vận tốc: v(2) = 3(2)² - 12(2) + 9 = 12 - 24 + 9 = -3 (m/s)

Vậy vận tốc của vật thể tại thời điểm t = 2 giây là -3 m/s.

Lưu ý khi giải bài tập 4.61

Đơn vị: Luôn chú ý đến đơn vị của các đại lượng trong bài toán và đảm bảo rằng kết quả cuối cùng có đơn vị phù hợp.
Kiểm tra lại: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Hiểu bản chất: Quan trọng nhất là hiểu bản chất của bài toán và vận dụng kiến thức một cách linh hoạt.

Bài tập tương tự và luyện tập

Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 11 Kết nối tri thức. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến hoặc tham gia các diễn đàn học tập để trao đổi kinh nghiệm và học hỏi lẫn nhau.

Tusach.vn – Đồng hành cùng các em trên con đường học tập

Tusach.vn luôn nỗ lực cung cấp những tài liệu học tập chất lượng, đáp ứng nhu cầu của học sinh. Chúng tôi hy vọng rằng bài giải chi tiết bài 4.61 trang 74 SBT Toán 11 Kết nối tri thức này sẽ giúp các em học tập tốt hơn. Chúc các em thành công!

Chủ đề	Nội dung
Kiến thức liên quan	Đạo hàm, đạo hàm của hàm hợp, đạo hàm của hàm lượng giác
Kỹ năng cần thiết	Tính đạo hàm, giải phương trình, phân tích bài toán