Giải bài 7.7 trang 28 SBT Toán 11 - Kết nối tri thức

Giải bài 7.7 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.7 trang 28 SBT Toán 11 - Kết nối tri thức

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 7.7 trang 28 sách bài tập Toán 11 Kết nối tri thức. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.

Chúng tôi luôn cập nhật nhanh chóng và đầy đủ đáp án các bài tập trong sách bài tập Toán 11 Kết nối tri thức, hỗ trợ tối đa cho quá trình học tập của bạn.

Cho tứ diện \(OABC\) có ba cạnh \(OA,OB,OC\) đôi một vuông góc với nhau.

Đề bài

Cho tứ diện \(OABC\) có ba cạnh \(OA,OB,OC\) đôi một vuông góc với nhau. Gọi \(H\) là chân đường vuông góc hạ từ \(O\) đến mặt phẳng\(\left( {ABC} \right)\). Chứng minh rằng:

a)\(BC \bot \left( {OAH} \right)\);

b) \(H\) là trực tâm của tam giác \(ABC\);

c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).

Phương pháp giải - Xem chi tiết Giải bài 7.7 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Áp dụng định lý sau

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng

một mặt phẳng thì nó vuông góc với mặt phẳng đó.

Chứng minh hai đường thẳng vuông góc dựa vào đường thẳng vuông góc với mặt phẳng

+ \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \subset \alpha \end{array} \right. \Rightarrow a \bot b\)

Áp dụng hệ thức lượng trong tam giác vuông

a) Chứng minh \(OA \bot BC\), \(OH \bot BC\).

b) Chứng minh \(BC \bot AH\), \(CA \bot BH\) suy ra \(H\) là trực tâm của tam giác \(ABC\).

c) + Gọi \(K\) là giao điểm của \(AH\) và \(BC\),

+ Chứng minh \(OK\) là đường cao của tam giác vuông \(OBC\) và \(OH\) là đường cao của tam giác vuông \(OAK\).

+ Áp dụng hệ thức lượng trong các tam giác vuông \(OBC\) và \(OAK\)

Lời giải chi tiết

a) Vì \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right)\), suy ra. \(OA \bot BC\)

Vì \(OH \bot \left( {ABC} \right)\) nên\(OH \bot BC\),suy ra\(BC \bot \left( {OAH} \right)\).

b) Vì \(BC \bot \left( {OAH} \right)\) nên \(BC \bot AH\).

Tương tự, \(CA \bot BH\), do đó \(H\) là trực tâm của tam giác\(ABC\).

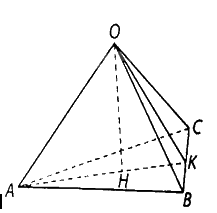
Giải bài 7.7 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

c) Gọi \(K\) là giao điểm của \(AH\) và \(BC\),

Ta có: \(OK \bot BC\) và \(OA \bot OK\) nên \(OK\) là đường cao của tam giác vuông \(OBC\) và là đường cao của tam giác vuông \(OAK\).

Áp dụng hệ thức lượng trong các tam giác vuông \(OBC\) và\(OAK\), ta có: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{K^2}}}\) và \(\frac{1}{{O{K^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).

Từ đó suy ra: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).

Giải bài 7.7 trang 28 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp giải

Bài 7.7 trang 28 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về Đạo hàm của hàm số. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm để giải quyết các bài toán liên quan đến tính đạo hàm của hàm số, tìm cực trị, và khảo sát hàm số.

Nội dung bài tập 7.7 trang 28 SBT Toán 11 - Kết nối tri thức

Bài 7.7 thường bao gồm các dạng bài tập sau:

Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số đơn thức, đa thức, và các hàm số phức tạp hơn.
Tìm đạo hàm cấp hai: Tính đạo hàm bậc hai của hàm số.
Ứng dụng đạo hàm để giải quyết các bài toán thực tế: Ví dụ như tìm vận tốc, gia tốc, hoặc tối ưu hóa các bài toán kinh tế.

Lời giải chi tiết bài 7.7 trang 28 SBT Toán 11 - Kết nối tri thức

Để giải bài 7.7 trang 28 SBT Toán 11 Kết nối tri thức một cách hiệu quả, bạn cần nắm vững các công thức và quy tắc đạo hàm cơ bản. Dưới đây là một số công thức quan trọng:

Đạo hàm của hàm số lũy thừa: (xⁿ)' = nx^n-1
Đạo hàm của hàm số lượng giác: (sin x)' = cos x, (cos x)' = -sin x
Đạo hàm của hàm số mũ và logarit: (e^x)' = e^x, (ln x)' = 1/x

Ví dụ minh họa:

Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = 3x² + 2x - 1. Ta thực hiện như sau:

f'(x) = (3x²)' + (2x)' - (1)' = 6x + 2 - 0 = 6x + 2

Mẹo giải bài tập đạo hàm Toán 11

Nắm vững các công thức đạo hàm cơ bản: Đây là nền tảng để giải quyết mọi bài tập về đạo hàm.
Sử dụng quy tắc chuỗi: Khi tính đạo hàm của hàm hợp, hãy áp dụng quy tắc chuỗi một cách chính xác.
Biến đổi biểu thức trước khi tính đạo hàm: Đôi khi, việc biến đổi biểu thức trước khi tính đạo hàm có thể giúp đơn giản hóa bài toán.
Kiểm tra lại kết quả: Sau khi tính đạo hàm, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Tusach.vn - Hỗ trợ học tập Toán 11 hiệu quả

Tusach.vn không chỉ cung cấp lời giải chi tiết bài 7.7 trang 28 SBT Toán 11 Kết nối tri thức mà còn cung cấp đầy đủ đáp án và lời giải của tất cả các bài tập trong sách bài tập Toán 11 Kết nối tri thức. Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất.

Ngoài ra, Tusach.vn còn cung cấp các tài liệu học tập hữu ích khác như:

Bài giảng Toán 11: Được trình bày một cách dễ hiểu, trực quan.
Bài tập trắc nghiệm Toán 11: Giúp bạn rèn luyện kỹ năng làm bài trắc nghiệm.
Các dạng bài tập Toán 11 thường gặp: Giúp bạn nắm vững các kiến thức trọng tâm.

Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kết quả học tập của bạn!

Giải bài 7.7 trang 28 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.7 trang 28 SBT Toán 11 - Kết nối tri thức

Giải bài 7.7 trang 28 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp giải

Nội dung bài tập 7.7 trang 28 SBT Toán 11 - Kết nối tri thức

Lời giải chi tiết bài 7.7 trang 28 SBT Toán 11 - Kết nối tri thức

Mẹo giải bài tập đạo hàm Toán 11

Tusach.vn - Hỗ trợ học tập Toán 11 hiệu quả

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN