Giải bài 1.29 trang 24 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 1.29 trang 24 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 1.29 trang 24 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học tập tốt hơn.
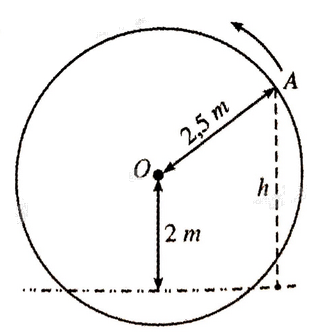
Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên).
Đề bài
Một chiếc guồng nước có dạng hình tròn bán kính 2,5m; trục của nó đặt cách mặt nước 2m (hình bên). Khi guồng quay đều, khoảng cách h (mét) tính từ một chiếc gầu gắn tại điểm A trên guồng đến mặt nước là \(h = \left| y \right|\) trong đó \(y = 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right)\) với x là thời gian quay của guồng \(\left( {x \ge 0} \right),\) tính bằng phút; ta quy ước rằng \(y > 0\) khi gầu ở trên mặt nước và \(y < 0\) khi gầu ở dưới mặt nước.
a) Khi nào chiếc gầu ở vị trí cao nhất? Thấp nhất?
b) Chiếc gầu cách mặt nước 2 mét lần đầu tiên khi nào?
Phương pháp giải - Xem chi tiết
* Sử dụng kiến thức \( - 1 \le \sin x \le 1\) với mọi x
* Sử dụng cách giải phương trình \(\sin x = m\) (1)
+ Nếu \(\left| m \right| > 1\) thì phương trình (1) vô nghiệm.
+ Nếu \(\left| m \right| \le 1\) thì tồn tại duy nhất số \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thỏa mãn \(\sin \alpha = m\).
Khi đó, phương trình (1) tương đương với:
\(\sin x = m \Leftrightarrow \sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết
a) Vì \( - 1 \le \sin 2\pi \left( {x - \frac{1}{4}} \right) \le 1\) nên \( - 2,5 \le 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 2,5\)
Do đó, \( - 0,5 = 2 - 2,5 \le 2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) \le 2 + 2,5 = 4,5\;\forall x \in \mathbb{R}\)
Suy ra, gầu ở vị trí cao nhất khi \(\sin 2\pi \left( {x - \frac{1}{4}} \right) = 1 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{1}{2} + k\left( {k \in \mathbb{Z}} \right)\)
Vì gầu ở vị trí cao nhất tại các thời điểm \(\frac{1}{2},\frac{3}{2},\frac{5}{2},...\) phút
Tương tự, gầu ở vị trí thấp nhất khi \(\sin 2\pi \left( {x - \frac{1}{4}} \right) = - 1 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = - \frac{\pi }{2} + k2\pi \Leftrightarrow x = k\left( {k \in \mathbb{Z}} \right)\)
Vì gầu ở vị trí cao nhất tại các thời điểm 0, 1, 2, 3… phút
b) Gầu cách mặt nước 2m khi \(2 + 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) = 2 \Leftrightarrow 2,5\sin 2\pi \left( {x - \frac{1}{4}} \right) = 0 \Leftrightarrow 2\pi \left( {x - \frac{1}{4}} \right) = k\pi \Leftrightarrow x = \frac{1}{4} + \frac{k}{2}\left( {k \in \mathbb{Z}} \right)\)
Vậy chiếc gầu cách mặt nước 2m lần đầu tại thời điểm \(x = \frac{1}{4}\) phút
Giải bài 1.29 trang 24 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 1.29 trang 24 sách bài tập Toán 11 Kết nối tri thức thuộc chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định của hàm số và các phép biến đổi hàm số để giải quyết. Việc nắm vững các khái niệm và phương pháp giải bài tập trong chương này là rất quan trọng để xây dựng nền tảng vững chắc cho các chương học tiếp theo.
Nội dung bài tập 1.29
Bài 1.29 yêu cầu học sinh xác định tập xác định của hàm số. Cụ thể, bài tập đưa ra một số hàm số và yêu cầu học sinh tìm ra các giá trị của x mà hàm số có nghĩa. Để giải bài tập này, học sinh cần nắm vững các điều kiện xác định của các hàm số cơ bản như hàm số phân thức, hàm số căn bậc hai, hàm số logarit,…
Lời giải chi tiết bài 1.29 trang 24 SBT Toán 11 - Kết nối tri thức
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 1.29:
Câu a)
Hàm số: y = √(2x - 1)
Điều kiện xác định: 2x - 1 ≥ 0
Giải bất phương trình: 2x ≥ 1 => x ≥ 1/2
Vậy tập xác định của hàm số là: D = [1/2; +∞)
Câu b)
Hàm số: y = 1 / (x - 3)
Điều kiện xác định: x - 3 ≠ 0
Giải phương trình: x ≠ 3
Vậy tập xác định của hàm số là: D = R \ {3}
Câu c)
Hàm số: y = log₂(x + 2)
Điều kiện xác định: x + 2 > 0
Giải bất phương trình: x > -2
Vậy tập xác định của hàm số là: D = (-2; +∞)
Phương pháp giải bài tập về tập xác định của hàm số
- Xác định các điều kiện xác định của từng loại hàm số thành phần: Ví dụ, với hàm số phân thức, mẫu số phải khác 0; với hàm số căn bậc hai, biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0; với hàm số logarit, biểu thức trong logarit phải lớn hơn 0.
- Giải các bất phương trình hoặc phương trình để tìm ra các giá trị của x thỏa mãn các điều kiện xác định.
- Kết hợp các điều kiện xác định để tìm ra tập xác định của hàm số.
Lưu ý khi giải bài tập
Khi giải bài tập về tập xác định của hàm số, cần chú ý:
- Đọc kỹ đề bài để xác định đúng hàm số cần tìm tập xác định.
- Nắm vững các điều kiện xác định của từng loại hàm số thành phần.
- Thực hiện các phép biến đổi toán học một cách chính xác.
- Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
Bài tập tương tự
Để củng cố kiến thức về tập xác định của hàm số, các em có thể làm thêm các bài tập tương tự trong sách bài tập Toán 11 Kết nối tri thức hoặc trên các trang web học tập trực tuyến.
Kết luận
Hy vọng bài giải chi tiết bài 1.29 trang 24 SBT Toán 11 - Kết nối tri thức này sẽ giúp các em hiểu rõ hơn về cách giải bài tập về tập xác định của hàm số. Chúc các em học tập tốt!