Giải bài 7.24 trang 34 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.24 trang 34 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 7.24 trang 34 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học tập tốt hơn.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, biết \(\left( {SAB} \right) \bot \left( {ABCD} \right)\), \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SA = a\). Tính côsin của số đo góc nhị diện \(\left[ {S,BD,C} \right]\) và góc nhị diện \(\left[ {B,SC,D} \right]\).
Phương pháp giải - Xem chi tiết
Để tính góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) ta có thể thực hiện cách sau:
Tìm hai đường thẳng \(a,b\) lần lượt vuông góc với hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
Khi đó góc giữa hai đường thẳng \(a,b\) chính là góc giữa hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\).
\(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \bot \left( \beta \right)\end{array} \right. \Rightarrow \widehat {\left( {\left( \alpha \right),\left( \beta \right)} \right)} = \widehat {\left( {a,b} \right)}\).
Áp dụng tính chất: Hình vuông có hai đường chéo vuông góc
Dựa vào tỉ số lượng giác trong tam giác vuông để tìm góc
Áp dụng định lí côsin trong tam giác
Lời giải chi tiết
Ta có \(SO \bot BD,CO \bot BD\) nên góc nhị diện \(\left[ {S,BD,C} \right]\) bằng \(\widehat {SOC}\).
Vì tam giác \(SAO\) vuông tại \(A\) nên \(SO = \sqrt {S{A^2} + A{O^2}} = \frac{{a\sqrt 6 }}{2}\) và \({\rm{cos}}\widehat {SOC} = - {\rm{cos}}\widehat {SOA} = - \frac{{OA}}{{SO}} = - \frac{{\sqrt 3 }}{3}\).
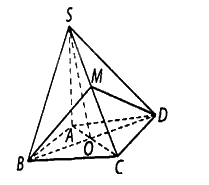
Kẻ \(BM \bot SC\) tại \(M\) thì \(DM \bot SC\) nên \(\left[ {B,SC,D} \right] = \widehat {BMD}\).
Ta có \(BC \bot \left( {SAB} \right)\) nên tam giác \(SBC\) vuông tại \(B\), tính được \(SB = a\sqrt 2 \), \(SC = a\sqrt 3 \) và \(DM = BM = \frac{{SB \cdot BC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\).
Áp dụng định lí côsin trong tam giác \(BDM\), ta có: \({\rm{cos}}\widehat {BMD} = \frac{{B{M^2} + D{M^2} - B{D^2}}}{{2 \cdot BM \cdot DM}} = - \frac{3}{4}\).
Giải bài 7.24 trang 34 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 7.24 trang 34 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế. Việc nắm vững các công thức đạo hàm cơ bản và kỹ năng tính đạo hàm là rất quan trọng để hoàn thành tốt bài tập này.
Nội dung bài tập 7.24
Bài 7.24 thường xoay quanh việc tính đạo hàm của các hàm số lượng giác, hàm số mũ, hàm số logarit hoặc các hàm số phức tạp hơn được xây dựng từ các hàm số cơ bản. Đôi khi, bài tập còn yêu cầu học sinh tìm đạo hàm cấp hai hoặc đạo hàm của hàm hợp.
Phương pháp giải bài tập 7.24
Để giải bài tập 7.24 hiệu quả, các em có thể áp dụng các phương pháp sau:
- Xác định đúng công thức đạo hàm cần sử dụng: Tùy thuộc vào dạng hàm số, các em cần chọn công thức đạo hàm phù hợp.
- Áp dụng quy tắc đạo hàm: Sử dụng các quy tắc đạo hàm như quy tắc cộng, trừ, nhân, chia, quy tắc chuỗi để tính đạo hàm của hàm số.
- Rút gọn biểu thức: Sau khi tính đạo hàm, các em cần rút gọn biểu thức để có được kết quả cuối cùng.
- Kiểm tra lại kết quả: Để đảm bảo tính chính xác, các em nên kiểm tra lại kết quả bằng cách tính đạo hàm lại hoặc thay các giá trị cụ thể vào hàm số.
Lời giải chi tiết bài 7.24 trang 34 SBT Toán 11 - Kết nối tri thức
Đề bài: (Giả sử đề bài là: Tính đạo hàm của hàm số f(x) = sin(2x) + ex)
Lời giải:
f'(x) = (sin(2x))' + (ex)'
f'(x) = cos(2x) * 2 + ex
f'(x) = 2cos(2x) + ex
Ví dụ minh họa khác
Đề bài: Tính đạo hàm của hàm số g(x) = ln(x2 + 1)
Lời giải:
g'(x) = (ln(x2 + 1))'
g'(x) = (1/(x2 + 1)) * (x2 + 1)'
g'(x) = (1/(x2 + 1)) * 2x
g'(x) = 2x/(x2 + 1)
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững các công thức đạo hàm cơ bản.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra kết quả.
- Tham khảo các tài liệu học tập và bài giải trên mạng để hiểu rõ hơn về cách giải bài tập.
Tusach.vn - Đồng hành cùng các em trên con đường học tập
Tusach.vn luôn cập nhật những bài giải mới nhất và chính xác nhất cho các bài tập trong sách bài tập Toán 11 Kết nối tri thức. Hãy truy cập website của chúng tôi để tìm kiếm lời giải cho các bài tập khác và nâng cao kiến thức Toán học của bạn!
| Công thức đạo hàm cơ bản | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x3)' = 3x2 |
| (sin x)' = cos x | (sin 2x)' = 2cos 2x |
| (cos x)' = -sin x | (cos x)' = -sin x |
| (ex)' = ex | (e2x)' = 2e2x |