Giải bài 7.32 trang 38 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7.32 trang 38 SBT Toán 11 Kết nối tri thức
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 7.32 trang 38 sách bài tập Toán 11 Kết nối tri thức. Bài giải bao gồm các bước thực hiện rõ ràng, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách bài tập Toán 11 Kết nối tri thức, hỗ trợ tối đa cho quá trình học tập của bạn.
Trên một mái nhà nghiêng \({30^ \circ }\) so với mặt phẳng nằm ngang, người ta dựng một chiếc cột vuông góc với mái nhà
Đề bài
Trên một mái nhà nghiêng \({30^ \circ }\) so với mặt phẳng nằm ngang, người ta dựng một chiếc cột vuông góc với mái nhà. Hỏi chiếc cột tạo với mặt phẳng nằm ngang một góc bao nhiêu độ? Vì sao?
Phương pháp giải - Xem chi tiết
Vẽ hình minh họa
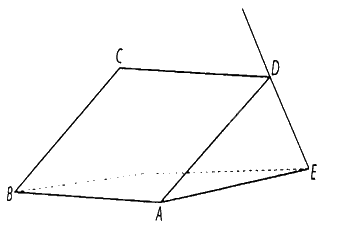
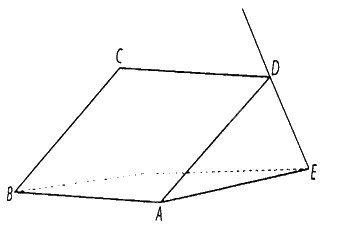
Gọi \(AB\) là giao tuyến của mặt phẳng mái nhà và mặt phẳng nằm ngang, \(AD\) là đường thẳng nằm trên mái nhà và vuông góc với \(AB\),
\(DE\) là chiếc cột vuông góc với mái nhà,
\(AE\) nằm trên mặt phẳng nằm ngang, khi đó tam giác \(ADE\) vuông tại \(D\), đường thẳng \(AE\) là hình chiếu vuông góc của \(DE\) trên mặt phẳng nằm ngang
Tính góc \(\widehat {DEA}\)
Lời giải chi tiết
Gọi \(AB\) là giao tuyến của mặt phẳng mái nhà và mặt phẳng nằm ngang, \(AD\) là đường thẳng nằm trên mái nhà và vuông góc với \(AB\), đường thẳng \(DE\) là chiếc cột vuông góc với mái nhà, đường thẳng \(AE\) nằm trên mặt phẳng nằm ngang, khi đó tam giác \(ADE\) vuông tại \(D\), đường thẳng \(AE\) là hình chiếu vuông góc của \(DE\) trên mặt phẳng nằm ngang, mà góc \(\widehat {DAE}\) bằng \({30^ \circ }\) nên góc giữa hai đường thẳng \(DE\) và \(AE\) bằng \({60^ \circ }\).
Vậy góc giữa đường thẳng \(DE\) (chiếc cột) và mặt phẳng nằm ngang bằng góc giữa hai đường \(DE\) và \(AE\) bằng \({60^ \circ }\)
Giải bài 7.32 trang 38 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp giải
Bài 7.32 trang 38 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về Đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Để giải quyết bài 7.32 một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Định nghĩa đạo hàm: Hiểu rõ đạo hàm của một hàm số tại một điểm là gì và cách tính đạo hàm bằng định nghĩa.
- Quy tắc tính đạo hàm: Nắm vững các quy tắc tính đạo hàm của các hàm số cơ bản (hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit) và quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Ứng dụng của đạo hàm: Biết cách sử dụng đạo hàm để tìm cực trị của hàm số, khảo sát hàm số, và giải các bài toán liên quan đến tốc độ biến thiên.
Lời giải chi tiết bài 7.32 trang 38 SBT Toán 11 Kết nối tri thức
Đề bài: (Giả sử đề bài là: Tìm đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1)
Lời giải:
- Áp dụng quy tắc đạo hàm của tổng, hiệu, và lũy thừa, ta có:
- f'(x) = d/dx (x3) - d/dx (2x2) + d/dx (5x) - d/dx (1)
- f'(x) = 3x2 - 4x + 5 - 0
- Vậy, f'(x) = 3x2 - 4x + 5
Các dạng bài tập tương tự và phương pháp giải
Ngoài bài 7.32, sách bài tập Toán 11 Kết nối tri thức còn nhiều bài tập tương tự về đạo hàm. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
- Bài tập tính đạo hàm: Yêu cầu tính đạo hàm của một hàm số cho trước. Phương pháp giải là áp dụng các quy tắc tính đạo hàm đã học.
- Bài tập tìm đạo hàm cấp hai: Yêu cầu tìm đạo hàm cấp hai của một hàm số. Phương pháp giải là tính đạo hàm cấp một trước, sau đó tính đạo hàm của đạo hàm cấp một.
- Bài tập ứng dụng đạo hàm: Yêu cầu sử dụng đạo hàm để giải quyết các bài toán thực tế, như tìm cực trị của hàm số, khảo sát hàm số, và giải các bài toán liên quan đến tốc độ biến thiên.
Lưu ý khi giải bài tập về đạo hàm
Để giải bài tập về đạo hàm một cách chính xác và hiệu quả, bạn cần lưu ý những điều sau:
- Nắm vững các định nghĩa và quy tắc: Đảm bảo bạn hiểu rõ các định nghĩa và quy tắc tính đạo hàm trước khi bắt đầu giải bài tập.
- Thực hành thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
- Sử dụng các công cụ hỗ trợ: Nếu cần thiết, bạn có thể sử dụng các công cụ hỗ trợ tính đạo hàm trực tuyến để kiểm tra kết quả của mình.
Tusach.vn – Đồng hành cùng bạn trên con đường chinh phục Toán học
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập môn Toán. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết, và các công cụ hỗ trợ giúp bạn học Toán hiệu quả hơn. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!