Giải bài 6.56 trang 22 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 6.56 trang 22 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu đến các em lời giải chi tiết bài 6.56 trang 22 sách bài tập Toán 11 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm.
Chúng tôi sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Vẽ đồ thị của hai hàm số \(y = {e^x}\) và \(y = {\rm{ln}}x\) trên cùng một hệ trục toạ độ.
Đề bài
a) Vẽ đồ thị của hai hàm số \(y = {e^x}\) và \(y = {\rm{ln}}x\) trên cùng một hệ trục toạ độ.
b) Chứng minh rằng hai đồ thị trên đối xứng nhau qua đường thẳng \(y = x\) tức điểm \(M\) nằm trên một đồ thị thì \(M'\) đối xứng với \(M\) qua đường thẳng \(y = x\) sẽ nằm trên đồ thị còn lại.
Phương pháp giải - Xem chi tiết
a) Để vẽ đồ thị ta làm như sau:
Lập bảng giá trị
Xác định các điểm trên mặt phẳng tọa độ rồi nối các điểm đó lại
b) Xét điểm \(A\left( {{x_0},{e^{{x_0}}}} \right)\) nằm trên đồ thị hàm số \(y = {e^x}\).
Viết phương trình đường thằng d đi qua \(A\) vuông góc với đường thẳng \(y = x\):
Toạ độ giao điểm của đường thẳng \({\rm{d}}\) và đường thẳng \(y = x\) là điểm \(B\)
Gọi \(A'\) là điểm đối xứng của \(A\) qua đường thằng \(y = x\). Ta tìm được tọa độ \(A'\). Khi đó chứng minh\(A'\) thuộc đồ thị hàm số \(y = {\rm{ln}}x\).
Tương tự nếu điểm \(B\left( {{x_0}{\rm{;ln}}{x_0}} \right)\) nằm trền đồ thị hàm số \(y = {\rm{ln}}x\) thì ta cũng có thể tìm toạ độ của điềm \(B'\) đối xứng với \(B\) qua đường thẳng \(y = x\) và chứng minh \(B'\) thuộc đồ thị hàm số \(y = {\theta ^x}\).
Vậy hai đồ thị đã cho đối xứng với nhau qua đường thẳng \(y = x\).
Lời giải chi tiết
a) Đồ thị của hai hàm số \(y = {e^x}\) và \(y = {\rm{ln}}x\) trên cùng một hệ trục toạ độ như hình sau:
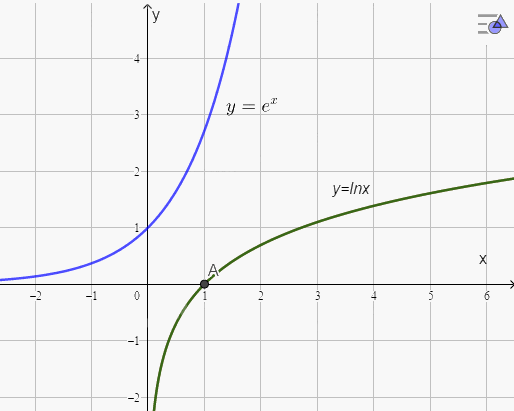
b) Xét điểm \(A\left( {{x_0},{e^{{x_0}}}} \right)\) nằm trên đồ thị hàm số \(y = {e^x}\).
Viết phương trình đường thằng đi qua \(A\) vuông góc với đường thẳng \(y = x\):
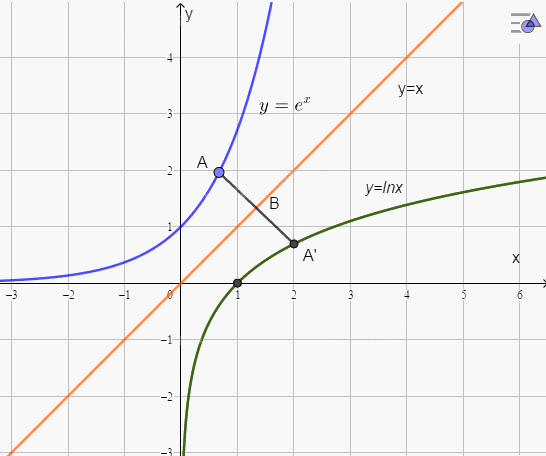
Toạ độ giao điểm của đường thẳng \({\rm{d}}\) và đường thẳng \(y = x\) là \(B\left( {\frac{{{x_0} + {e^{{x_0}}}}}{2};\frac{{{x_0} + {e^{{x_0}}}}}{2}} \right)\)
Gọi \(A'\) là điểm đối xứng của \(A\) qua đường thằng \(y = x\). Ta tìm được \(A'\left( {{e^{{x_0}}};{x_0}} \right)\). Khi đó \(A'\) thuộc đồ thị hàm số \(y = {\rm{ln}}x\). Tương tự nếu điếm \(B\left( {{x_0}{\rm{;ln}}{x_0}} \right)\) nằm trền đồ thị hàm số \(y = {\rm{ln}}x\) thì ta cũng có thể tìm toạ độ của điềm \(B'\) đối xứng với \(B\) qua đường thẳng \(y = x\) và chứng minh \(B'\) thuộc đồ thị hàm số \(y = {e^x}\).
Vậy hai đồ thị đã cho đối xứng với nhau qua đường thẳng \(y = x\).
Chú ý: Tổng quát, có thề chứng minh rằng đồ thị của hai hàm số \(y = {a^x}\) và \(y = {\rm{lo}}{{\rm{g}}_a}x(0 < a \ne 1)\) đối xứng với nhau qua đường phân giác của góc phẩn tư thứ nhất (tức là đường thẳng \(y = x\) ).
Giải bài 6.56 trang 22 SBT Toán 11 - Kết nối tri thức: Hướng dẫn chi tiết
Bài 6.56 trang 22 sách bài tập Toán 11 Kết nối tri thức yêu cầu chúng ta tìm đạo hàm của hàm số. Để giải bài này, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản như đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp.
Đề bài:
Tìm đạo hàm của các hàm số sau:
- y = x3 - 3x2 + 2x - 5
- y = (x2 + 1)(x - 2)
- y = 1/x2
- y = sin(2x)
Lời giải chi tiết:
y = x3 - 3x2 + 2x - 5
y' = 3x2 - 6x + 2
y = (x2 + 1)(x - 2)
y' = (2x)(x - 2) + (x2 + 1)(1)
y' = 2x2 - 4x + x2 + 1
y' = 3x2 - 4x + 1
y = 1/x2 = x-2
y' = -2x-3 = -2/x3
y = sin(2x)
y' = cos(2x) * 2 = 2cos(2x)
Lưu ý quan trọng:
- Khi tính đạo hàm của tích hai hàm số, ta sử dụng quy tắc đạo hàm của tích: (uv)' = u'v + uv'
- Khi tính đạo hàm của hàm hợp, ta sử dụng quy tắc đạo hàm của hàm hợp: (f(g(x)))' = f'(g(x)) * g'(x)
- Luôn kiểm tra lại kết quả đạo hàm để đảm bảo tính chính xác.
Mở rộng kiến thức:
Ngoài bài 6.56, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 11 Kết nối tri thức để rèn luyện kỹ năng tính đạo hàm. Việc nắm vững các quy tắc đạo hàm là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Tusach.vn - Đồng hành cùng các em học Toán 11!
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong sách giáo khoa và sách bài tập Toán 11 Kết nối tri thức. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất trong quá trình học tập!
| Bài tập | Đáp án |
|---|---|
| 6.56a | 3x2 - 6x + 2 |
| 6.56b | 3x2 - 4x + 1 |
| 6.56c | -2/x3 |
| 6.56d | 2cos(2x) |