Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 4.31 trang 67 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
SBT Toán 11 - Kết nối tri thức
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Chương IV. Quan hệ song song trong không gian
Bài 13. Hai mặt phẳng song song

Giải bài 4.31 trang 67 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 4.31 trang 67 SBT Toán 11 - Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 4.31 trang 67 sách bài tập Toán 11 Kết nối tri thức. Bài tập này thuộc chương trình học Toán 11, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.

Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.

. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E là một điểm bất kì thuộc cạnh SA và (P) là mặt phẳng qua E song song với mặt phẳng (ABCD).

a) Xác định giao tuyến của mặt phẳng (P) và các mặt bên của hình chóp.

b) Hình tạo bởi các giao tuyến là hình gì? Giải thích vì sao.

Phương pháp giải - Xem chi tiếtGiải bài 4.31 trang 67 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a song song với b.

Cho hai mặt phẳng song song, nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.

Lời giải chi tiết

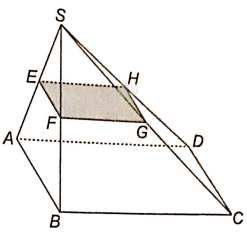
Giải bài 4.31 trang 67 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

a) Trong mặt phẳng (SAB), qua E kẻ đường thẳng song song với AB cắt SB tại F. Khi đó, EF là giao tuyến của mặt phẳng (P) và mặt phẳng (SAB).

Trong mặt phẳng (SBC), qua F kẻ đường thẳng song song với BC cắt SC tại G. Khi đó, FG là giao tuyến của mặt phẳng (P) và mặt phẳng (SBC).

Trong mặt phẳng (SCD), qua G kẻ đường thẳng song song với DC cắt SD tại H. Khi đó, GH là giao tuyến của mặt phẳng (P) và mặt phẳng (SCD).

Vì E vừa thuộc mặt phẳng (P) vừa thuộc mặt phẳng (SAD); H vừa thuộc mặt phẳng (P) vừa thuộc mặt phẳng (SAD) nên EH là giao tuyến của (P) và mặt phẳng (SAD)

b) Vì mp (ABCD)//mp (EFGH), EH là giao tuyến của mp (EFGH) và mp (SAD), AD là giao tuyến của mp (ABCD) và mp (SAD) nên EH//AB.

Vì EH//AD, AD//BC nên EH//BC

Mà FG//BC nên EH//FG

Vì EF//AB, AB//CD nên EF//DC

Mà HG//DC nên EF//HG

Tứ giác EFGH có: EF//GH, EH//FG nên tứ giác EFGH là hình bình hành.

Giải bài 4.31 trang 67 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp

Bài 4.31 trang 67 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Để giải bài tập này một cách hiệu quả, các em cần nắm vững các khái niệm cơ bản như đạo hàm, cực trị, điểm uốn và cách sử dụng đạo hàm để tìm ra các yếu tố này.

Nội dung bài tập 4.31

Bài tập 4.31 thường yêu cầu học sinh thực hiện các công việc sau:

  • Tính đạo hàm của hàm số.
  • Tìm các điểm cực trị của hàm số.
  • Xác định khoảng đồng biến, nghịch biến của hàm số.
  • Tìm điểm uốn của hàm số.
  • Vẽ đồ thị hàm số.

Phương pháp giải bài tập 4.31

Để giải bài tập 4.31 một cách hiệu quả, các em có thể áp dụng các bước sau:

  1. Bước 1: Tính đạo hàm cấp một của hàm số.
  2. Bước 2: Tìm các điểm mà đạo hàm cấp một bằng 0 hoặc không xác định. Đây là các điểm nghi ngờ là điểm cực trị.
  3. Bước 3: Khảo sát dấu của đạo hàm cấp một trên các khoảng xác định để xác định khoảng đồng biến, nghịch biến của hàm số.
  4. Bước 4: Tính đạo hàm cấp hai của hàm số.
  5. Bước 5: Tìm các điểm mà đạo hàm cấp hai bằng 0 hoặc không xác định. Đây là các điểm nghi ngờ là điểm uốn.
  6. Bước 6: Khảo sát dấu của đạo hàm cấp hai trên các khoảng xác định để xác định tính lồi, lõm của hàm số.
  7. Bước 7: Dựa vào các kết quả trên để vẽ đồ thị hàm số.

Lời giải chi tiết bài 4.31 trang 67 SBT Toán 11 - Kết nối tri thức

(Ở đây sẽ là lời giải chi tiết của bài tập 4.31. Ví dụ minh họa)

Ví dụ: Xét hàm số y = x3 - 3x2 + 2.

Bước 1: Tính đạo hàm cấp một: y' = 3x2 - 6x.

Bước 2: Tìm các điểm cực trị: y' = 0 ⇔ 3x2 - 6x = 0 ⇔ x = 0 hoặc x = 2.

Bước 3: Khảo sát dấu của y':

x-∞02+∞
y'+-+
yĐồng biếnNghịch biếnĐồng biến

Vậy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2). Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 2.

Lưu ý khi giải bài tập 4.31

  • Luôn kiểm tra điều kiện xác định của hàm số trước khi tính đạo hàm.
  • Sử dụng các quy tắc đạo hàm một cách chính xác.
  • Khảo sát dấu của đạo hàm một cách cẩn thận để xác định khoảng đồng biến, nghịch biến và các điểm cực trị.
  • Vẽ đồ thị hàm số để kiểm tra lại kết quả.

Hy vọng với lời giải chi tiết và phương pháp giải bài tập 4.31 trang 67 SBT Toán 11 Kết nối tri thức này, các em sẽ hiểu rõ hơn về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Chúc các em học tập tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN