Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 20 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
SBT Toán 11 - Kết nối tri thức
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Bài tập ôn tập cuối năm

Giải bài 20 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 20 trang 69 SBT Toán 11 - Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết bài 20 trang 69 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.

Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp những tài liệu học tập chất lượng và dễ hiểu nhất.

Cho hình chóp \(S.ABCD\) có mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy \(\left( {ABCD} \right)\)

Đề bài

Cho hình chóp \(S.ABCD\) có mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy \(\left( {ABCD} \right)\), tam giác \(SAB\) đều, đáy \(ABCD\) là hình vuông cạnh bằng \(a\). Gọi \(H\) là trung điểm của cạnh \(AB\). Khoảng cách từ điểm \(H\) đến mặt phẳng \(\left( {SAC} \right)\) bằng

A. \(\frac{{a\sqrt {30} }}{5}\).

B. \(\frac{{a\sqrt {21} }}{{14}}\).

C. \(\frac{{a\sqrt 6 }}{{10}}\).

D. \(\frac{{a\sqrt 6 }}{5}\).

Phương pháp giải - Xem chi tiếtGiải bài 20 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Chứng minh \(SH \bot \left( {ABCD} \right)\), tính \(SH\)

Dựng hình chiếu \(K\) của \(H\) trên \(\left( {SAC} \right)\).

Tính \(HK\)

Lời giải chi tiết

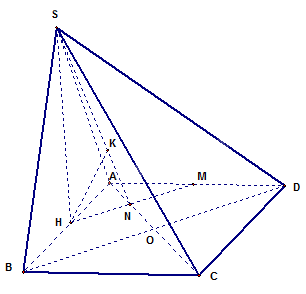
Giải bài 20 trang 69 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

Ta có \(AC \bot BD;AC = a\sqrt 2 \);

Gọi \(M\) là trung điểm của \(AD\) và \(HM \cap AC = N\).

Do \(\Delta SAB\) là tam giác đều nên \(SH \bot AB;SH = \frac{{a\sqrt 3 }}{2}\).

Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right) \Rightarrow SH \bot AC\) ;

\(HM\) là đường trung bình tam giác \(ABD \Rightarrow HM//BD \Rightarrow HM \bot AC\)

\(HN = \frac{1}{2}HM = \frac{1}{4}AC = \frac{{a\sqrt 2 }}{4}\)

Vì \(SH \bot AC;HN \bot AC \Rightarrow \left( {SHN} \right) \bot AC\)

Kẻ \(HK \bot SN\) tại \(K\).

Ta chứng minh được \(HK \bot SN;AC \Rightarrow HK \bot \left( {SAC} \right)\) tại \(K\).

Suy ra: \(d\left( {H,\left( {SAC} \right)} \right) = HK\).

Ta có: \(HK = \frac{{HS.HN}}{{\sqrt {H{S^2} + H{N^2}} }}\) \( = \frac{{\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 2 }}{4}}}{{\sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 2 }}{4}} \right)}^2}} }}\)\( = \frac{{a\sqrt {21} }}{{14}}\).

Chọn C

Giải bài 20 trang 69 SBT Toán 11 - Kết nối tri thức: Tổng quan

Bài 20 trang 69 sách bài tập Toán 11 Kết nối tri thức tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập bao gồm các dạng bài tập về xác định tập xác định của hàm số, tìm tập giá trị, xét tính đơn điệu, tìm cực trị và vẽ đồ thị hàm số lượng giác. Việc nắm vững kiến thức về hàm số lượng giác là vô cùng quan trọng, không chỉ cho các bài kiểm tra trong chương mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.

Nội dung chi tiết bài 20 trang 69 SBT Toán 11 - Kết nối tri thức

Bài 20 bao gồm nhiều câu hỏi nhỏ, mỗi câu hỏi tập trung vào một khía cạnh khác nhau của hàm số lượng giác. Dưới đây là phân tích chi tiết từng dạng bài và phương pháp giải:

1. Xác định tập xác định của hàm số lượng giác

Để xác định tập xác định của hàm số lượng giác, cần lưu ý các điều kiện sau:

  • Mẫu số khác 0
  • Biểu thức dưới dấu căn bậc chẵn lớn hơn hoặc bằng 0
  • Biểu thức trong logarit lớn hơn 0

Ví dụ: Hàm số y = 1/(sin x - cos x) có tập xác định là tập hợp tất cả các x sao cho sin x ≠ cos x, tức là x ≠ π/4 + kπ (k ∈ Z).

2. Tìm tập giá trị của hàm số lượng giác

Tập giá trị của hàm số lượng giác thường được xác định bằng cách sử dụng các tính chất của hàm số và các giá trị lớn nhất, nhỏ nhất của hàm số. Ví dụ, tập giá trị của hàm số y = sin x là [-1, 1].

3. Xét tính đơn điệu của hàm số lượng giác

Để xét tính đơn điệu của hàm số lượng giác, có thể sử dụng đạo hàm của hàm số. Nếu đạo hàm dương trên một khoảng thì hàm số đồng biến trên khoảng đó, và nếu đạo hàm âm trên một khoảng thì hàm số nghịch biến trên khoảng đó.

4. Tìm cực trị của hàm số lượng giác

Cực trị của hàm số lượng giác được tìm bằng cách giải phương trình đạo hàm bằng 0 và xét dấu của đạo hàm cấp hai. Nếu đạo hàm cấp hai dương tại một điểm thì điểm đó là điểm cực tiểu, và nếu đạo hàm cấp hai âm tại một điểm thì điểm đó là điểm cực đại.

Lời giải chi tiết các bài tập trong bài 20 trang 69 SBT Toán 11 - Kết nối tri thức

Dưới đây là lời giải chi tiết cho từng bài tập trong bài 20 trang 69 sách bài tập Toán 11 Kết nối tri thức:

  1. Bài 20.1: ... (Giải chi tiết)
  2. Bài 20.2: ... (Giải chi tiết)
  3. Bài 20.3: ... (Giải chi tiết)
  4. ...

Mẹo giải nhanh các bài tập hàm số lượng giác

  • Nắm vững các công thức lượng giác cơ bản.
  • Sử dụng đạo hàm để xét tính đơn điệu và tìm cực trị.
  • Vẽ đồ thị hàm số để hiểu rõ hơn về tính chất của hàm số.
  • Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.

Tài liệu tham khảo hữu ích

Ngoài sách bài tập, các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán:

  • Sách giáo khoa Toán 11 - Kết nối tri thức
  • Các trang web học Toán trực tuyến
  • Các video bài giảng trên YouTube

Hy vọng bài viết này đã giúp các em hiểu rõ hơn về bài 20 trang 69 sách bài tập Toán 11 Kết nối tri thức. Chúc các em học tập tốt!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN