Giải bài 7.25 trang 35 Sách bài tập Toán 11 - Kết nối tri thức

Giải bài 7.25 trang 35 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.25 trang 35 SBT Toán 11 Kết nối tri thức

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 7.25 trang 35 sách bài tập Toán 11 Kết nối tri thức. Bài giải bao gồm các bước thực hiện rõ ràng, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập.

Chúng tôi luôn cập nhật nhanh chóng và chính xác đáp án các bài tập trong sách bài tập Toán 11 Kết nối tri thức, hỗ trợ tối đa cho quá trình học tập của bạn.

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\)

Đề bài

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), tam giác \(SAD\) đều và nằm trong mặt phẳng vuông góc với mặt đáy \(\left( {ABCD} \right)\). Gọi \(H,M\) lần lượt là trung điểm của các cạnh \(AD\) và \(AB\).

a) Tính côsin của góc giữa đường thẳng \(SC\) và mặt đáy \(\left( {ABCD} \right)\).

b) Chứng minh rằng \(\left( {SMD} \right) \bot \left( {SHC} \right)\).

Phương pháp giải - Xem chi tiết Giải bài 7.25 trang 35 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

Áp dụng tính chất:

Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng và vuông góc với giao tyến cũng vuông góc với mặt phẳng kia.

\(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\a \subset \left( P \right)\\b = \left( P \right) \cap \left( Q \right)\\a \bot b\end{array} \right. \Rightarrow a \bot \left( Q \right)\)

Giải bài 7.25 trang 35 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

Ta có \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SH \bot AD\) nên \(SH \bot \left( {ABCD} \right)\),

Xác định hình chiếu của đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\)

Tính góc giữa hai đường thẳng \({\rm{SC}}\) và hình chiếu của nó rồi kết luận

Để chứng minh \(\left( {SDM} \right) \bot \left( {SCH} \right)\) sử dụng tính chất \(DM \bot CH,DM \bot SH\)

Lời giải chi tiết

a) Ta có \(\left( {SAD} \right) \bot \left( {ABCD} \right)\) và \(SH \bot AD\) nên \(SH \bot \left( {ABCD} \right)\), suy ra góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng góc giữa hai đường thẳng \({\rm{SC}}\) và \({\rm{CH}}\), mà \(\left( {{\rm{SC}},{\rm{CH}}} \right) = \widehat {{\rm{SCH}}}\), ta tính được \(SH = \frac{{a\sqrt 3 }}{2},HC = \frac{{a\sqrt 5 }}{2}\) và \(SC = a\sqrt 2 \).

Do đó \({\rm{cos}}\widehat {SHC} = \frac{{HC}}{{SC}} = \frac{{\sqrt {10} }}{4}\).

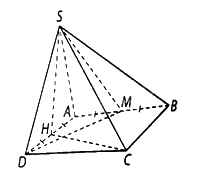
Giải bài 7.25 trang 35 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 3

b) Ta có \(DM \bot CH,DM \bot SH\) nên \(DM \bot \left( {SCH} \right)\). Hơn nữa, mặt phẳng (SDM) chứa đường thẳng \(DM\) nên \(\left( {SDM} \right) \bot \left( {SCH} \right)\).

Giải bài 7.25 trang 35 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp giải

Bài 7.25 trang 35 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số, đặc biệt là đạo hàm của các hàm số lượng giác và hàm hợp để giải quyết các bài toán liên quan đến tiếp tuyến của đường cong.

Nội dung bài tập 7.25 trang 35 SBT Toán 11 Kết nối tri thức

Bài tập 7.25 thường có dạng như sau: Cho hàm số y = f(x). Tìm phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = a. Để giải bài tập này, học sinh cần thực hiện các bước sau:

Tính đạo hàm f'(x) của hàm số y = f(x).
Tính f'(a) để tìm hệ số góc k của tiếp tuyến tại điểm có hoành độ x = a.
Tính tung độ y₀ = f(a) của điểm tiếp xúc.
Viết phương trình tiếp tuyến theo công thức: y - y₀ = k(x - a).

Ví dụ minh họa giải bài 7.25 trang 35 SBT Toán 11 Kết nối tri thức

Ví dụ: Cho hàm số y = sin(2x). Tìm phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = π/4.

Tính đạo hàm: y' = 2cos(2x)
Tính f'(π/4): y'(π/4) = 2cos(2 * π/4) = 2cos(π/2) = 0
Tính f(π/4): y(π/4) = sin(2 * π/4) = sin(π/2) = 1
Phương trình tiếp tuyến: y - 1 = 0(x - π/4) => y = 1

Lưu ý khi giải bài tập 7.25 trang 35 SBT Toán 11 Kết nối tri thức

Nắm vững các công thức đạo hàm cơ bản của các hàm số lượng giác (sin x, cos x, tan x, cot x).
Sử dụng thuần thạo quy tắc đạo hàm của hàm hợp.
Kiểm tra lại kết quả tính toán để tránh sai sót.
Chú ý đến đơn vị của góc khi tính đạo hàm của các hàm số lượng giác.

Tusach.vn – Hỗ trợ học tập Toán 11 hiệu quả

Tusach.vn không chỉ cung cấp lời giải chi tiết bài 7.25 trang 35 SBT Toán 11 Kết nối tri thức mà còn hỗ trợ giải các bài tập khác trong chương trình Toán 11. Chúng tôi cam kết mang đến cho bạn những tài liệu học tập chất lượng, chính xác và dễ hiểu. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Bảng tổng hợp công thức đạo hàm thường dùng

Hàm số y = f(x)	Đạo hàm y' = f'(x)
sin x	cos x
cos x	-sin x
tan x	1/cos² x
cot x	-1/sin² x