Giải bài 6.22 trang 14 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 6.22 trang 14 SBT Toán 11 Kết nối tri thức
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 6.22 trang 14 sách bài tập Toán 11 Kết nối tri thức. Bài giải được các thầy cô giáo có kinh nghiệm biên soạn, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập tốt nhất, hỗ trợ học sinh ôn tập và làm bài tập hiệu quả.
Vẽ đồ thị của các hàm số lôgarit sau:
Đề bài
Vẽ đồ thị của các hàm số lôgarit sau:
a) \({\rm{lo}}{{\rm{g}}_{\sqrt 3 }}x\)
b) \(y = {\rm{lo}}{{\rm{g}}_{\frac{2}{3}}}x\)
Phương pháp giải - Xem chi tiết
Hàm số lôgarit \(y = {\rm{lo}}{{\rm{g}}_a}x\):
- Có tập xác định là \(\left( {0; + \infty } \right)\) và tập giá trị là \(\mathbb{R}\);
- Liên tục trên \(\left( {0; + \infty } \right)\);
- Có đồ thị đi qua các điểm \(\left( {1;0} \right),\left( {a;1} \right)\) và luôn nằm bên phải trục tung.
- Dạng đồ thị của hàm số \(y = {\rm{lo}}{{\rm{g}}_a}x\)
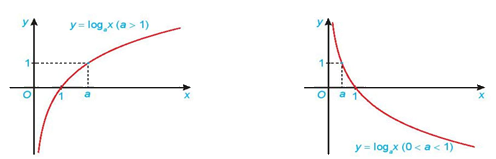
Vẽ đồ thị hàm số \(y = {\log _a}x\).
Lập bảng giá trị của hàm số tại một số điểm như sau:

Xác định các điểm có tọa độ theo bảng trên
Từ đó, ta vẽ được đồ thị của hàm số \(y = {\log _a}x\)
Lời giải chi tiết
a) Lập bảng giá trị của hàm số tại một số điểm như sau:
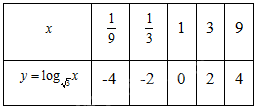
Từ đó, ta vẽ được đồ thị của hàm số \(y = {\rm{lo}}{{\rm{g}}_{\sqrt 3 }}x\) như hình sau;
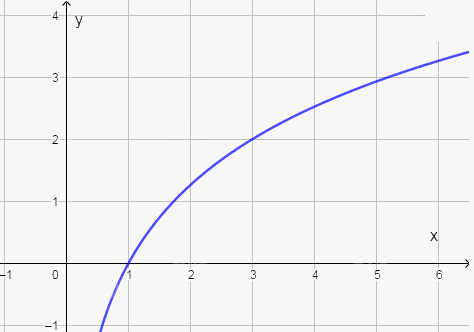
b) Lập bảng giá tri của hàm số tại một số điểm như sau:
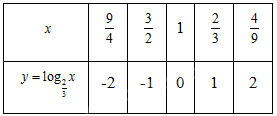
Từ đó, ta vẽ được đồ thị của hàm số \(y = {\rm{lo}}{{\rm{g}}_{\frac{2}{3}}}x\) như hình sau:
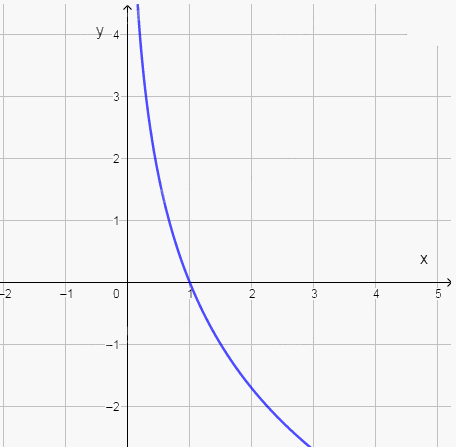
Giải bài 6.22 trang 14 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp giải
Bài 6.22 trang 14 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về phép biến hình. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán liên quan đến hình học.
Nội dung bài tập 6.22 trang 14 SBT Toán 11 Kết nối tri thức
Bài tập 6.22 thường có dạng như sau:
- Cho một hình H và một phép biến hình f. Tìm ảnh H' của hình H qua phép biến hình f.
- Xác định tâm, góc, trục của phép biến hình f dựa trên hình H và ảnh H'.
- Chứng minh một điểm hoặc một đường thẳng bất kỳ là bất biến qua một phép biến hình.
Phương pháp giải bài tập 6.22 trang 14 SBT Toán 11 Kết nối tri thức
- Xác định rõ phép biến hình: Đọc kỹ đề bài để xác định chính xác loại phép biến hình được sử dụng (tịnh tiến, quay, đối xứng trục, đối xứng tâm).
- Nắm vững tính chất của phép biến hình: Mỗi phép biến hình có những tính chất riêng. Ví dụ, phép tịnh tiến bảo toàn khoảng cách giữa hai điểm, phép quay bảo toàn góc giữa hai đường thẳng.
- Sử dụng công thức biến hình: Áp dụng công thức biến hình tương ứng để tìm tọa độ của ảnh sau phép biến hình.
- Vẽ hình minh họa: Vẽ hình minh họa giúp hình dung rõ hơn về bài toán và kiểm tra tính hợp lý của kết quả.
- Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Ví dụ minh họa giải bài 6.22 trang 14 SBT Toán 11 Kết nối tri thức
Bài toán: Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến đó.
Giải:
Áp dụng công thức phép tịnh tiến: A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)
Thay số: A'(1 + 3; 2 - 1) = A'(4; 1)
Vậy, tọa độ điểm A' là (4; 1).
Lưu ý khi giải bài tập về phép biến hình
- Chú ý đến chiều của vectơ tịnh tiến, góc quay, trục đối xứng.
- Sử dụng hệ tọa độ để biểu diễn các điểm và vectơ.
- Kiểm tra kỹ các điều kiện của bài toán để tránh sai sót.
Tusach.vn – Hỗ trợ học tập Toán 11 hiệu quả
Tusach.vn không chỉ cung cấp lời giải chi tiết bài 6.22 trang 14 SBT Toán 11 Kết nối tri thức mà còn tổng hợp nhiều tài liệu học tập hữu ích khác như:
- Giải bài tập sách giáo khoa Toán 11 Kết nối tri thức
- Lý thuyết Toán 11 Kết nối tri thức
- Đề thi thử Toán 11
- Bài tập trắc nghiệm Toán 11
Hãy truy cập tusach.vn để học tập và ôn luyện Toán 11 hiệu quả nhất!
| Phép biến hình | Công thức biến hình |
|---|---|
| Tịnh tiến | A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b) |
| Quay | (Công thức quay phức tạp hơn, cần xem lại sách giáo khoa) |
| Đối xứng trục | (Công thức đối xứng trục phức tạp hơn, cần xem lại sách giáo khoa) |
| Đối xứng tâm | (Công thức đối xứng tâm phức tạp hơn, cần xem lại sách giáo khoa) |