Giải bài 1.42 trang 26 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 1.42 trang 26 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 1.42 trang 26 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học tập tốt hơn.
Khẳng định nào sau đây đúng?
Đề bài
Khẳng định nào sau đây đúng?
A. Hàm số \(y = \cos x\) nghịch biến trên khoảng \(( - \pi ;0)\) và đồng biến trên khoảng \((0;\pi )\).
B. Hàm số \(y = \cos x\) đồng biến trên các khoảng \(( - \pi ;0)\) và \((0;\pi )\).
C. Hàm số \(y = \cos x\) nghịch biến trên các khoảng \(( - \pi ;0)\) và \((0;\pi )\).
D. Hàm số \(y = \cos x\) đồng biến trên khoảng \(( - \pi ;0)\) và nghịch biến trên khoảng \((0;\pi )\).
Phương pháp giải - Xem chi tiết
Dựa vào lý thuyết hàm số \(y = \cos x\) đồng biến trên khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\).
Hoặc dựa vào đồ thị hàm số để khẳng định tính đồng biến nghịch biến của nó.
Lời giải chi tiết
Đáp án D.
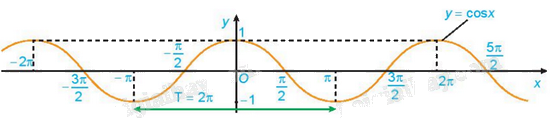
Dựa vào đồ thị, ta thấy hàm số \(y = \cos x\) đồng biến trên khoảng \(( - \pi ;0)\) và nghịch biến trên khoảng \((0;\pi )\).
Giải bài 1.42 trang 26 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 1.42 trang 26 sách bài tập Toán 11 Kết nối tri thức thuộc chương 1: Vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ và điều kiện vuông góc.
Nội dung bài tập 1.42
Bài 1.42 thường bao gồm các dạng bài tập sau:
- Tính tích vô hướng của hai vectơ.
- Tìm góc giữa hai vectơ.
- Xác định điều kiện để hai vectơ vuông góc.
- Ứng dụng tích vô hướng để giải các bài toán hình học.
Lời giải chi tiết bài 1.42 trang 26 SBT Toán 11 - Kết nối tri thức
Để giúp các em hiểu rõ hơn về cách giải bài tập này, Tusach.vn xin trình bày lời giải chi tiết như sau:
(Giả sử đề bài cụ thể của bài 1.42 là: Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính tích vô hướng của a và b.)
Lời giải:
Tích vô hướng của hai vectơ a = (x1; y1) và b = (x2; y2) được tính theo công thức:
a ⋅ b = x1x2 + y1y2
Trong trường hợp này, ta có:
a ⋅ b = (1)(-3) + (2)(4) = -3 + 8 = 5
Vậy, tích vô hướng của hai vectơ a và b là 5.
Các dạng bài tập tương tự và phương pháp giải
Ngoài bài 1.42, các em có thể gặp các bài tập tương tự như:
- Tìm m để hai vectơ vuông góc.
- Tính độ dài của vectơ.
- Chứng minh một góc bằng 90 độ.
Để giải các bài tập này, các em cần nắm vững các công thức và tính chất của tích vô hướng:
- a ⋅ b = |a||b|cos(θ), trong đó θ là góc giữa hai vectơ a và b.
- a ⊥ b ⇔ a ⋅ b = 0
- |a| = √(x2 + y2)
Mẹo giải nhanh
Để giải nhanh các bài tập về tích vô hướng, các em nên:
- Nắm vững các công thức và tính chất.
- Phân tích đề bài để xác định đúng dạng bài.
- Sử dụng máy tính bỏ túi để tính toán nhanh chóng.
Luyện tập thêm
Để củng cố kiến thức, các em nên luyện tập thêm các bài tập khác trong sách bài tập và các đề thi thử. Tusach.vn sẽ tiếp tục cập nhật thêm nhiều bài giải và tài liệu học tập hữu ích khác.
Kết luận
Hy vọng bài giải chi tiết bài 1.42 trang 26 SBT Toán 11 - Kết nối tri thức này sẽ giúp các em hiểu rõ hơn về kiến thức và kỹ năng giải bài tập. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| a ⋅ b = x1x2 + y1y2 | Tích vô hướng của hai vectơ |
| a ⋅ b = |a||b|cos(θ) | Mối quan hệ giữa tích vô hướng và góc giữa hai vectơ |