Giải bài 4.17 trang 59 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.17 trang 59 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Bài viết này của tusach.vn sẽ cung cấp lời giải chi tiết và dễ hiểu bài 4.17 trang 59 sách bài tập Toán 11 Kết nối tri thức. Chúng tôi hy vọng sẽ giúp các em hiểu rõ hơn về kiến thức và kỹ năng giải toán.
Bài 4.17 yêu cầu chúng ta vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.
Đề bài
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi G, H lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng GH, CE, DF đôi một song song.
Phương pháp giải - Xem chi tiết
Dựa vào tính chất hình bình hành và tính chất đường trung bình của tam giác chứng minh 3 đường thẳng song song
Lời giải chi tiết
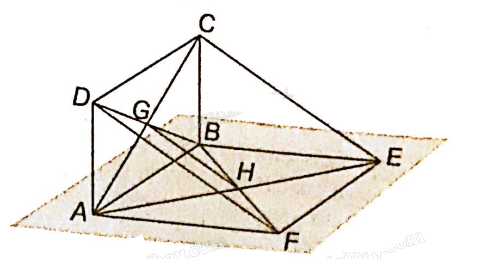
G là giao điểm hai đường chéo BD, AC của hình bình hành ABCD nên G là trung điểm của BD và AC.
H là giao điểm hai đường chéo BF, AE của hình bình hành ABEF nên H là trung điểm của BF và AE.
Xét tam giác BDF, GH là đường trung bình của tam giác nên GH song song với DF.
GH là đường trung bình tam giác ACE nên GH song song với CE.
Vậy ba đường thẳng GH, CE, DF đôi một song song.
Giải bài 4.17 trang 59 SBT Toán 11 - Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu
Bài 4.17 trang 59 sách bài tập Toán 11 Kết nối tri thức là một bài toán quan trọng, giúp học sinh củng cố kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Dưới đây là lời giải chi tiết và các bước thực hiện để các em có thể hiểu rõ hơn:
Đề bài:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Gọi M là trung điểm của CD.
- Chứng minh rằng BD vuông góc với AM.
- Tính góc giữa đường thẳng SM và mặt phẳng (ABCD).
- Tính khoảng cách từ C đến mặt phẳng (SAD).
Lời giải:
a) Chứng minh BD vuông góc với AM:
- Ta có: BD ⊥ AC (tính chất hình vuông).
- SA ⊥ (ABCD) ⇒ SA ⊥ BD.
- Do đó, BD ⊥ (SAC).
- Mặt khác, AM ⊂ (SAC) ⇒ BD ⊥ AM. (đpcm)
b) Tính góc giữa đường thẳng SM và mặt phẳng (ABCD):
- Vì SA ⊥ (ABCD) nên góc giữa SM và (ABCD) chính là góc SMA.
- Ta có: AM = √(AD² + DM²) = √(a² + (a/2)²) = (a√5)/2.
- Trong tam giác SAM vuông tại A, ta có: tan(SMA) = SA/AM = a / ((a√5)/2) = 2/√5.
- Vậy, góc giữa SM và (ABCD) là arcsin(2/√5) ≈ 63.43°.
c) Tính khoảng cách từ C đến mặt phẳng (SAD):
- Gọi H là hình chiếu vuông góc của C lên AD. Khi đó CH ⊥ AD.
- Vì SA ⊥ (ABCD) nên SA ⊥ CH.
- Do đó, CH ⊥ (SAD). Vậy khoảng cách từ C đến (SAD) chính là CH.
- Ta có: CH = CD = a.
Lưu ý quan trọng:
Khi giải các bài toán về hình không gian, việc vẽ hình chính xác và sử dụng các tính chất quan trọng như quan hệ vuông góc, song song là rất quan trọng. Hãy luôn kiểm tra lại các bước giải và đảm bảo rằng các kết quả thu được là hợp lý.
Mở rộng:
Các em có thể tìm hiểu thêm về các dạng bài tập tương tự trong sách giáo khoa và sách bài tập Toán 11 Kết nối tri thức để nâng cao kỹ năng giải toán. Ngoài ra, các em cũng có thể tham khảo các bài giảng trực tuyến và các tài liệu học tập khác để bổ sung kiến thức.
Tusach.vn hy vọng bài giải này sẽ giúp các em học tốt môn Toán 11. Chúc các em thành công!
| Khái niệm | Giải thích |
|---|---|
| Đường thẳng vuông góc với mặt phẳng | Đường thẳng tạo với mặt phẳng một góc 90 độ. |
| Góc giữa đường thẳng và mặt phẳng | Góc tạo bởi đường thẳng và hình chiếu của nó trên mặt phẳng. |
| Khoảng cách từ một điểm đến mặt phẳng | Độ dài đoạn vuông góc hạ từ điểm đó xuống mặt phẳng. |