Giải bài 7.44 trang 42 Sách bài tập Toán 11 - Kết nối tri thức

Giải bài 7.44 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Giải bài 7.44 trang 42 SBT Toán 11 Kết nối tri thức

Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 7.44 trang 42 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu hơn về kiến thức và rèn luyện kỹ năng giải toán.

Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, dễ hiểu, giúp các em học tập hiệu quả.

Cho tứ diện đều \(ABCD\)có cạnh bằng\(a\), côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\)bằng

Đề bài

Cho tứ diện đều \(ABCD\)có cạnh bằng\(a\), côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\)bằng

A. \(\frac{1}{3}\).

B. \(\frac{{\sqrt 3 }}{3}\).

C. \(\frac{{\sqrt 3 }}{2}\).

D. \(\frac{1}{2}\).

Phương pháp giải - Xem chi tiết Giải bài 7.44 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 1

- Chóp có các cạnh bên bằng nhau có chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.

- Góc giữa đường và mặt là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng.

- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.

Lời giải chi tiết

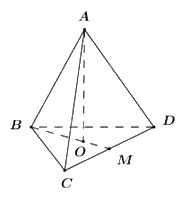
Giải bài 7.44 trang 42 sách bài tập toán 11 - Kết nối tri thức với cuộc sống 2

Gọi \(M\)là trung điểmcủa \(CD,O\) là tâm đường tròn ngoại tiếp tam giác đều \(BCD\)⇒\(AO \bot (BCD)\)

Khi đó \(OB\)là hình chiếu vuông góc của \(AB\) lên \((BCD)\)

\( \Rightarrow (AB;(BCD)) = (AB;OB) = \widehat {ABO}\)

Tam giác \(BCD\) đều cạnh a nên \(BM = \frac{{a\sqrt 3 }}{2} \Rightarrow BO = \frac{{2BM}}{3} = \frac{{a\sqrt 3 }}{3}\).

Ta có \(AO \bot (BCD)\) nên\(AO \bot OB\), suy ra \(\Delta ABO\)vuông tại \(O\).

⇒\(cos\widehat {ABO} = \frac{{OB}}{{AB}} = \frac{{\sqrt 3 }}{3}\)

Vậy \(\cos (AB;(BCD)) = \frac{{\sqrt 3 }}{3}\)

Giải bài 7.44 trang 42 SBT Toán 11 Kết nối tri thức: Tổng quan và Phương pháp

Bài 7.44 trang 42 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, đặc biệt là đạo hàm của hàm hợp và đạo hàm của hàm lượng giác để giải quyết các bài toán thực tế.

Nội dung bài tập 7.44

Bài 7.44 thường xoay quanh việc tính đạo hàm của các hàm số phức tạp, hoặc tìm điều kiện để hàm số có đạo hàm tại một điểm. Đôi khi, bài tập còn yêu cầu học sinh sử dụng đạo hàm để giải các bài toán liên quan đến tối ưu hóa, chẳng hạn như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Phương pháp giải bài tập 7.44

Xác định đúng công thức đạo hàm cần sử dụng: Đạo hàm của hàm số cơ bản (hàm số mũ, hàm số logarit, hàm lượng giác), quy tắc đạo hàm của hàm hợp, quy tắc đạo hàm của tích, thương, tổng, hiệu.
Biến đổi hàm số về dạng đơn giản: Sử dụng các tính chất của phép toán để biến đổi hàm số về dạng dễ tính đạo hàm hơn.
Tính đạo hàm từng bước một: Áp dụng các công thức đạo hàm một cách cẩn thận và chính xác.
Kiểm tra lại kết quả: Đảm bảo rằng kết quả đạo hàm của bạn là hợp lý và phù hợp với bài toán.

Giải chi tiết bài 7.44 trang 42 SBT Toán 11 Kết nối tri thức

(Ở đây sẽ là lời giải chi tiết của bài tập 7.44. Ví dụ minh họa, cần thay thế bằng lời giải thực tế)

Ví dụ: Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = sin(2x + 1).

Lời giải:

Đặt u = 2x + 1
Khi đó, f(x) = sin(u)
Đạo hàm của u theo x là: du/dx = 2
Đạo hàm của f theo u là: df/du = cos(u)
Áp dụng quy tắc đạo hàm của hàm hợp: df/dx = (df/du) * (du/dx) = cos(u) * 2 = 2cos(2x + 1)

Các dạng bài tập tương tự và cách giải

Ngoài bài 7.44, các em có thể gặp các bài tập tương tự như:

Tính đạo hàm của hàm số lượng giác phức tạp.
Tìm đạo hàm cấp hai của hàm số.
Sử dụng đạo hàm để giải các bài toán về cực trị của hàm số.

Để giải các bài tập này, các em cần nắm vững các kiến thức về đạo hàm và luyện tập thường xuyên. Tusach.vn sẽ cung cấp thêm nhiều bài giải chi tiết và các bài tập luyện tập để giúp các em nắm vững kiến thức hơn.

Lưu ý khi giải bài tập về đạo hàm

Luôn kiểm tra kỹ các công thức đạo hàm trước khi sử dụng.
Cẩn thận với các dấu ngoặc và phép toán.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi để kiểm tra kết quả.

Tusach.vn – Đồng hành cùng các em trên con đường học tập

Tusach.vn là website cung cấp giải bài tập, đáp án và kiến thức Toán học từ lớp 6 đến lớp 12. Chúng tôi luôn cố gắng mang đến cho các em những nội dung chất lượng, dễ hiểu và hữu ích. Hãy truy cập Tusach.vn để học tập và rèn luyện kiến thức Toán học một cách hiệu quả!