Giải bài 4.44 trang 71 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.44 trang 71 SBT Toán 11 - Kết nối tri thức
Chào các em học sinh! Tusach.vn xin giới thiệu bài giải chi tiết bài 4.44 trang 71 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, lời giải dễ hiểu và phương pháp giải bài tập hiệu quả.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp các em học tập tốt hơn.
. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN
Đề bài
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN. Gọi A’, B’, C’, D’, M’, N’ lần lượt là hình chiếu của A, B, C, D, M, N qua phép chiếu lên mặt phẳng (P) theo phương MN.
a) Chứng minh rằng hai điểm M’ và N’ trùng nhau.
b) Chứng minh rằng bốn điểm A’, B’, C’, D’ là bốn đỉnh của một hình bình hành.
Phương pháp giải - Xem chi tiết
- Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:
+ Nếu M thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và \(\Delta \).
+ Nếu M không thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và đường thẳng qua M song song với \(\Delta \).
Điểm M’ được gọi là hình chiếu của M trên mặt phẳng \(\left( \alpha \right)\) theo phương chiếu \(\Delta \).
- Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Lời giải chi tiết
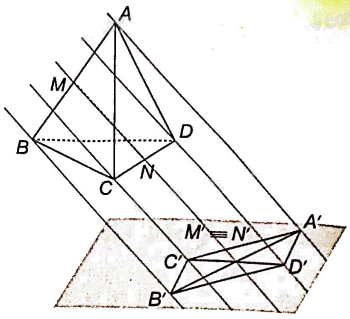
a) Vì đường thẳng MN là phương chiếu nên M’ của M trùng với hình chiếu N’ của N.
b) Vì M là trung điểm của AB nên theo tính chất của phép chiếu song song suy ra M’ là trung điểm của A’B’.
Vì N là trung điểm của CD nên theo tính chất của phép chiếu song song suy ra N’ là trung điểm của C’D’.
Vì M’ trùng N’ nên tứ giác tạo bởi bốn điểm A’, B’, C’, D’ có các đường chéo đi qua trung điểm của mỗi đường, suy ra tứ giác đó là hình bình hành.
Giải bài 4.44 trang 71 SBT Toán 11 - Kết nối tri thức: Tổng quan và Phương pháp
Bài 4.44 trang 71 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng, phương trình mặt phẳng để giải quyết các bài toán liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng, khoảng cách từ điểm đến mặt phẳng, và các bài toán ứng dụng thực tế.
Nội dung bài tập 4.44
Bài 4.44 thường bao gồm các dạng bài tập sau:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng (song song, vuông góc, cắt nhau).
- Tính góc giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ điểm đến mặt phẳng.
- Lập phương trình đường thẳng, mặt phẳng thỏa mãn các điều kiện cho trước.
Hướng dẫn giải bài 4.44 trang 71 SBT Toán 11 - Kết nối tri thức
Để giải quyết bài tập 4.44 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Vectơ chỉ phương của đường thẳng: Vectơ chỉ phương của đường thẳng d là vectơ khác vectơ không và cùng phương với đường thẳng d.
- Vectơ pháp tuyến của mặt phẳng: Vectơ pháp tuyến của mặt phẳng (P) là vectơ khác vectơ không và vuông góc với mọi vectơ nằm trong mặt phẳng (P).
- Phương trình đường thẳng: Có nhiều dạng phương trình đường thẳng, tùy thuộc vào thông tin đã cho (điểm đi qua và vectơ chỉ phương, hai điểm, giao điểm với các trục tọa độ,...).
- Phương trình mặt phẳng: Phương trình mặt phẳng có dạng Ax + By + Cz + D = 0, trong đó (A, B, C) là vectơ pháp tuyến của mặt phẳng.
- Điều kiện song song, vuông góc, cắt nhau giữa đường thẳng và mặt phẳng: Nắm vững các điều kiện này để xác định vị trí tương đối giữa đường thẳng và mặt phẳng.
- Công thức tính khoảng cách từ điểm đến mặt phẳng: d = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2), trong đó M(x0, y0, z0) là điểm và (P): Ax + By + Cz + D = 0 là mặt phẳng.
Ví dụ minh họa giải bài 4.44
Bài toán: Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa đường thẳng d và mặt phẳng (P).
Lời giải:
Vectơ chỉ phương của đường thẳng d là a = (1, -1, 2). Vectơ pháp tuyến của mặt phẳng (P) là n = (2, -1, 1).
Ta có a.n = 1*2 + (-1)*(-1) + 2*1 = 2 + 1 + 2 = 5 ≠ 0. Do đó, đường thẳng d và mặt phẳng (P) cắt nhau.
Lưu ý khi giải bài tập
- Đọc kỹ đề bài và xác định đúng các thông tin đã cho.
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
- Sử dụng các công thức và kiến thức đã học một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn - Đồng hành cùng các em học Toán
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong sách bài tập Toán 11 Kết nối tri thức. Hãy truy cập tusach.vn để học tập hiệu quả và đạt kết quả cao trong môn Toán!