Giải bài 4.30 trang 67 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.30 trang 67 SBT Toán 11 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 4.30 trang 67 sách bài tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho tứ diện ABCD và một điểm O nằm trong tam giác BCD. Gọi (P) là mặt phẳng qua O và song song với mặt phẳng (ABD).
Đề bài
Cho tứ diện ABCD và một điểm O nằm trong tam giác BCD. Gọi (P) là mặt phẳng qua O và song song với mặt phẳng (ABD).
a) Xác định giao tuyến của mặt phẳng (P) và mặt phẳng (BCD).
b) Xác định giao tuyến của mặt phẳng (P) và các mặt còn lại của tứ diện.
Phương pháp giải - Xem chi tiết
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a song song với b.
Lời giải chi tiết
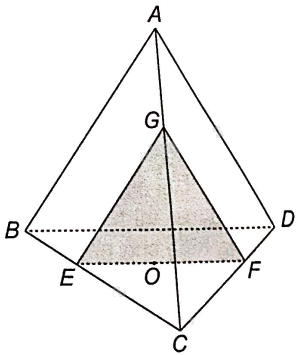
a) Qua O kẻ đường thẳng song song với BD cắt BC tại E, cắt CD tại F. Khi đó, EF là giao tuyến của mặt phẳng (P) và mặt phẳng (BCD).
b) Trong mặt phẳng (ABC), vẽ EG//AB (G thuộc AC) thì EG là giao tuyến của mặt phẳng (P) với mặt phẳng ABC.
Ta có: G thuộc AC nằm trong mặt phẳng ACD, F thuộc DC nằm trong mặt phẳng ACD. Khi đó, GF là giao tuyến của mặt phẳng (P) và mặt phẳng (ACD).
Giải bài 4.30 trang 67 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 4.30 trang 67 sách bài tập Toán 11 Kết nối tri thức thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, phương trình đường thẳng, phương trình mặt phẳng để giải quyết các bài toán liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng, khoảng cách từ điểm đến mặt phẳng, và các bài toán ứng dụng thực tế.
Nội dung bài tập 4.30
Bài 4.30 thường bao gồm các dạng bài tập sau:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng (song song, vuông góc, cắt nhau).
- Tính góc giữa đường thẳng và mặt phẳng.
- Tính khoảng cách từ điểm đến mặt phẳng.
- Lập phương trình đường thẳng, mặt phẳng thỏa mãn các điều kiện cho trước.
Lời giải chi tiết bài 4.30 trang 67 SBT Toán 11 - Kết nối tri thức
Để giải bài 4.30 trang 67 một cách hiệu quả, các em cần nắm vững các kiến thức sau:
- Vectơ chỉ phương của đường thẳng: Vectơ chỉ phương của đường thẳng d là vectơ khác vectơ không và cùng phương với đường thẳng d.
- Vectơ pháp tuyến của mặt phẳng: Vectơ pháp tuyến của mặt phẳng (P) là vectơ khác vectơ không và vuông góc với mọi vectơ nằm trong mặt phẳng (P).
- Phương trình đường thẳng: Có nhiều dạng phương trình đường thẳng, tùy thuộc vào thông tin đã cho (điểm đi qua và vectơ chỉ phương, hai điểm, giao điểm với các trục tọa độ,...).
- Phương trình mặt phẳng: Phương trình mặt phẳng có dạng Ax + By + Cz + D = 0, trong đó (A, B, C) là vectơ pháp tuyến của mặt phẳng.
- Điều kiện song song, vuông góc, cắt nhau giữa đường thẳng và mặt phẳng: Các em cần nắm vững các điều kiện này để xác định vị trí tương đối giữa đường thẳng và mặt phẳng.
- Công thức tính khoảng cách từ điểm đến mặt phẳng: d = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2), trong đó M(x0, y0, z0) là điểm và (P): Ax + By + Cz + D = 0 là mặt phẳng.
Ví dụ minh họa (giả định bài tập cụ thể):
Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa d và (P).
Lời giải:
Vectơ chỉ phương của d là a = (1, -1, 2). Vectơ pháp tuyến của (P) là n = (2, -1, 1). Ta có a.n = 1*2 + (-1)*(-1) + 2*1 = 5 ≠ 0. Do đó, đường thẳng d và mặt phẳng (P) cắt nhau.
Mẹo giải bài tập
- Vẽ hình minh họa để dễ dàng hình dung bài toán.
- Sử dụng các công thức một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
- Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.
Tusach.vn - Nguồn tài liệu học tập Toán 11 uy tín
Tusach.vn cung cấp đầy đủ lời giải chi tiết, bài tập trắc nghiệm và các tài liệu học tập Toán 11 khác. Hãy truy cập Tusach.vn để học Toán 11 hiệu quả hơn!
| Chương | Nội dung chính |
|---|---|
| 1 | Vectơ trong không gian |
| 2 | Đường thẳng và mặt phẳng trong không gian |
| 3 | Đạo hàm |