Câu 9 trang 35 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 9 Trang 35 SGK Hình Học 11 Nâng Cao
Câu 9 trang 35 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học Hình học không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các vấn đề liên quan đến chứng minh các đẳng thức vectơ.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.
Cho đường tròn (O ; R)
Đề bài
Cho đường tròn (O ; R) và điểm A cố định. Một dây cung BC thay đổi của (O ; R) có độ dài không đổi BC = m. Tìm quỹ tích các điểm G sao cho \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Lời giải chi tiết
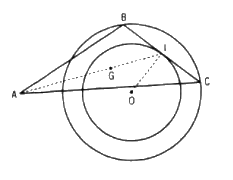
Gọi I là trung điểm của BC thì \(OI\bot BC\)
Ta có
\(\eqalign{& \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \cr & \Leftrightarrow \overrightarrow {GA} + 2\overrightarrow {GI} = \overrightarrow 0 \cr & \Leftrightarrow \overrightarrow {AG} = {2 \over 3}\overrightarrow {AI} \cr} \)
Tức là phép vị tự V tâm A tỉ số \({2 \over 3}\) biến điểm I thành điểm G
Trong tam giác vuông OIB ta có:
\(OI = \sqrt {O{B^2} - I{B^2}} \)\(= \sqrt {{R^2} - {{\left( {{m \over 2}} \right)}^2}} = R'\) (không đổi)
Nên quỹ tích I là đường tròn (O ; R’) hoặc là điểm O (nếu m = 2R)
Do đó quỹ tích G là ảnh của quỹ tích I qua phép vị tự V
Giải Chi Tiết Câu 9 Trang 35 SGK Hình Học 11 Nâng Cao
Câu 9 trang 35 SGK Hình học 11 Nâng cao thuộc chương trình học Hình học không gian, cụ thể là phần vectơ. Bài toán này thường yêu cầu học sinh chứng minh các đẳng thức vectơ, đòi hỏi sự hiểu biết vững chắc về các quy tắc cộng, trừ, nhân vectơ với một số thực, cũng như các tính chất của vectơ.
Nội Dung Bài Toán
Thông thường, câu 9 trang 35 sẽ đưa ra một hình không gian (ví dụ: hình hộp, hình chóp) và một số điểm trong hình đó. Sau đó, yêu cầu học sinh chứng minh một đẳng thức vectơ liên quan đến các vectơ được tạo bởi các điểm này. Ví dụ:
- Chứng minh rằng overrightarrow{AB} +overrightarrow{BC} =overrightarrow{AC}
- Chứng minh rằng overrightarrow{OA} +overrightarrow{OB} = 2overrightarrow{OM} (với M là trung điểm của AB)
Phương Pháp Giải
Để giải quyết bài toán này, học sinh cần nắm vững các phương pháp sau:
- Phân tích vectơ: Phân tích các vectơ thành các thành phần vectơ khác để đơn giản hóa bài toán.
- Sử dụng quy tắc cộng, trừ vectơ: Áp dụng quy tắc cộng, trừ vectơ để biến đổi các biểu thức vectơ.
- Sử dụng tính chất của vectơ: Vận dụng các tính chất của vectơ như tính giao hoán, tính kết hợp, tính chất phân phối để chứng minh đẳng thức.
- Sử dụng hình học: Kết hợp kiến thức hình học để xác định mối quan hệ giữa các vectơ.
Ví Dụ Minh Họa
Giả sử đề bài yêu cầu chứng minh overrightarrow{AB} +overrightarrow{CD} =overrightarrow{AD} +overrightarrow{CB} trong hình bình hành ABCD.
Lời giải:
Ta có:
- overrightarrow{AB} =overrightarrow{DC} (do ABCD là hình bình hành)
- overrightarrow{CD} = -overrightarrow{DC}
Do đó:
overrightarrow{AB} +overrightarrow{CD} =overrightarrow{DC} -overrightarrow{DC} =overrightarrow{0}
Tương tự:
- overrightarrow{AD} =overrightarrow{BC} (do ABCD là hình bình hành)
- overrightarrow{CB} = -overrightarrow{BC}
Do đó:
overrightarrow{AD} +overrightarrow{CB} =overrightarrow{BC} -overrightarrow{BC} =overrightarrow{0}
Vậy, overrightarrow{AB} +overrightarrow{CD} =overrightarrow{AD} +overrightarrow{CB} (đều bằng overrightarrow{0})
Lưu Ý Quan Trọng
Khi giải các bài toán về vectơ, cần chú ý:
- Vẽ hình minh họa để dễ hình dung bài toán.
- Sử dụng đúng các quy tắc và tính chất của vectơ.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn - Nguồn Tài Liệu Học Tập Uy Tín
Tusach.vn cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong SGK Hình học 11 Nâng cao. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các tài liệu học tập hữu ích để giúp các em học sinh học tốt môn Hình học. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Chúc các em học tập tốt!