Giải Câu 35 Trang 68 SGK Hình Học 11 Nâng Cao

Câu 35 trang 68 SGK Hình học 11 Nâng cao

Giải Bài Tập Hình Học 11 Nâng Cao - Câu 35 Trang 68

Câu 35 trang 68 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian để giải quyết các vấn đề thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho ({{IM} over {IN}} = k,k ne 0)cho trước

Đề bài

Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k,k \ne 0\)cho trước

Lời giải chi tiết

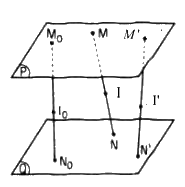
Câu 35 trang 68 SGK Hình học 11 Nâng cao 1

Thuận. Giả sử M \(\in\) (P), N \(\in\) (Q) và điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k.\)

Trên hai mặt phẳng (P) và (Q), ta lần lượt lấy hai điểm cố định M₀ và N₀ rồi lấy một điểm I₀ thuộc đoạn thẳng M₀N₀ sao cho \({{{M_0}{I_0}} \over {{N_0}{I_0}}} = k.\) Khi ấy điểm I₀ cố định.

Ta có: \({{IM} \over {IN}} = {{{I_0}{M_0}} \over {{I_0}{N_0}}}\left( { = k} \right)\)

\(\Rightarrow {{IM} \over {{I_0}{M_0}}} = {{IN} \over {{I_0}{N_0}}} = {{IM + IN} \over {{I_0}{M_0} + {I_0}{N_0}}} = {{MN} \over {{M_0}{N_0}}}\)

Áp dụng định lí Ta-lét đảo, ta suy ra đường thẳng I₀I thuộc một mặt phẳng (R) song song với (P) và (Q).

Mặt phẳng (R) cố định vì nó qua điểm cố định I₀ và song song với mặt phẳng cố định (P).

Vậy điểm I thuộc mặt phẳng (R) cố định.

Đảo. Ngược lại, lấy một điểm I’ bất kì trên mặt phẳng (R).

Qua I’ ta kẻ một đường thẳng cắt hai mặt phẳng (P) và (Q) lần lượt tại M’ và N’.

Xét hai cát tuyến M₀N₀ , M’N’ và ba mặt phẳng song song (P), (Q), (R).

Theo định lí Ta-lét ta có: \({{I'M'} \over {{I_0}{M_0}}} = {{I'N'} \over {{I_0}{N_0}}} = {{M'N'} \over {{M_0}{N_0}}}\)

Từ đó, ta suy ra I' thuộc đoạn thẳng M’N’ và \({{I'M'} \over {I'N'}} = {{{I_0}{M_0}} \over {{I_0}{N_0}}} = k\)

Kết luận: Tập hợp điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k\) là mặt phẳng (R) nói trên.

Giải Chi Tiết Câu 35 Trang 68 SGK Hình Học 11 Nâng Cao

Câu 35 trang 68 SGK Hình học 11 Nâng cao thường xoay quanh các bài toán liên quan đến việc xác định mối quan hệ giữa đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ chỉ phương của đường thẳng, vectơ pháp tuyến của mặt phẳng, điều kiện song song, vuông góc, cắt nhau giữa đường thẳng và mặt phẳng.

Tóm Tắt Lý Thuyết Quan Trọng

Vectơ chỉ phương của đường thẳng: Một vectơ chỉ phương của đường thẳng là một vectơ song song với đường thẳng đó.
Vectơ pháp tuyến của mặt phẳng: Một vectơ pháp tuyến của mặt phẳng là một vectơ vuông góc với mọi vectơ nằm trong mặt phẳng đó.
Điều kiện song song: Đường thẳng song song với mặt phẳng khi và chỉ khi vectơ chỉ phương của đường thẳng vuông góc với vectơ pháp tuyến của mặt phẳng.
Điều kiện vuông góc: Đường thẳng vuông góc với mặt phẳng khi và chỉ khi vectơ chỉ phương của đường thẳng cùng phương với vectơ pháp tuyến của mặt phẳng.
Điều kiện cắt nhau: Đường thẳng cắt mặt phẳng khi và chỉ khi vectơ chỉ phương của đường thẳng không vuông góc với vectơ pháp tuyến của mặt phẳng.

Phân Tích Đề Bài Câu 35 Trang 68

Để giải quyết Câu 35 trang 68, trước hết, cần đọc kỹ đề bài và xác định rõ các yếu tố đã cho: phương trình đường thẳng, phương trình mặt phẳng, và yêu cầu của bài toán (ví dụ: xác định góc giữa đường thẳng và mặt phẳng, tìm giao điểm của đường thẳng và mặt phẳng, chứng minh một mối quan hệ nào đó). Sau đó, áp dụng các công thức và kiến thức đã học để giải quyết bài toán.

Ví Dụ Minh Họa (Giả định một dạng bài tập phổ biến)

Đề bài: Cho đường thẳng (d): x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa đường thẳng (d) và mặt phẳng (P).

Giải:

Tìm vectơ chỉ phương của đường thẳng (d): a = (1, -1, 2)
Tìm vectơ pháp tuyến của mặt phẳng (P): n = (2, -1, 1)
Tính tích vô hướng của a và n: a.n = (1)(2) + (-1)(-1) + (2)(1) = 2 + 1 + 2 = 5
Kết luận: Vì a.n ≠ 0, nên đường thẳng (d) và mặt phẳng (P) cắt nhau.

Lưu Ý Khi Giải Bài Tập

Luôn kiểm tra lại các phép tính để tránh sai sót.
Vẽ hình minh họa để dễ dàng hình dung bài toán.
Sử dụng các công thức và định lý một cách chính xác.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng.

Tusach.vn - Hỗ Trợ Học Tập Hình Học 11 Nâng Cao

Tusach.vn là một nguồn tài liệu học tập hữu ích cho học sinh lớp 11. Chúng tôi cung cấp lời giải chi tiết, bài tập trắc nghiệm, và các tài liệu tham khảo khác để giúp các em học tốt môn Hình học. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!

Ngoài ra, đừng quên tham khảo các bài giải khác của SGK Hình học 11 Nâng cao tại tusach.vn để củng cố kiến thức và chuẩn bị tốt cho các kỳ thi.

Chương	Bài	Liên kết
1	1	Câu 1 Trang 8
1	2	Câu 2 Trang 8