Đề bài
Cho tam giác ABC vuông tại A, AB = a, BC = 2a. Hai tia Bx và Cy cùng vuông góc với mp(ABC) và nằm về một phía đối với mặt phẳng đó. Trên Bx, Cy lần lượt lấy các điểm B’, C’ sao cho BB’ = a, CC’ = m.
a. Với giá trị nào của m thì AB’C’ là tam giác vuông ?
b. Khi tam giác AB’C’ vuông tại B’, kẻ AH ⊥ BC. Chứng minh rằng B’C’H là tam giác vuông. Tính góc giữa hai mặt phẳng (ABC) và (AB’C’).
Lời giải chi tiết
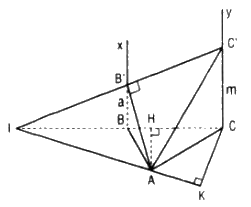
\(\Delta ABC\) vuông tại A nên theo pitago:
\(A{C^2} = B{C^2} - A{B^2}\) \( = {\left( {2a} \right)^2} - {a^2} = 3{a^2}\)
Tam giác ABB’ vuông tại B nên theo pitago:
\(AB{'^2} = A{B^2} + BB{'^2}\) \( = {a^2} + {a^2} = 2{a^2}\)
Tam giác ACC’ vuông tại C nên theo pitago:
\(AC{'^2} = A{C^2} + CC{'^2} = 3{a^2} + {m^2}\)
Trong (BCC’B’), kẻ \(B'M \bot CC'\) thì \(B'M = 2a,MC' = m - a\)
Tam giác B’MC’ vuông tại M nên theo pitago:
\(B'C{'^2} = B'{M^2} + MC{'^2}\) \( = {\left( {2a} \right)^2} + {\left( {m - a} \right)^2} = 4{a^2} + {\left( {m - a} \right)^2}\)
a. Ta có:
+) Tam giác AB’C’ vuông ở A khi và chỉ khi:
\(\begin{array}{l}AB{'^2} + AC{'^2} = B'C{'^2}\\ \Leftrightarrow 2{a^2} + 3{a^2} + {m^2} = 4{a^2} + {\left( {m - a} \right)^2}\\ \Leftrightarrow 5{a^2} + {m^2} = 4{a^2} + {m^2} - 2ma + {a^2}\\ \Leftrightarrow 2ma = 0\\ \Leftrightarrow m = 0\end{array}\)
Vậy tam giác AB’C’ vuông ở A khi và chỉ khi m = 0
+) Tam giác AB’C’ vuông ở C’ khi và chỉ khi :
\(\begin{array}{l}AC{'^2} + B'C{'^2} = AB{'^2}\\ \Leftrightarrow 3{a^2} + {m^2} + 4{a^2} + {\left( {m - a} \right)^2} = 2{a^2}\\ \Leftrightarrow 5{a^2} + {m^2} + {\left( {m - a} \right)^2} = 0\end{array}\)
Điều này không xảy ra vì:
\(\left\{ \begin{array}{l}5{a^2} > 0\\{m^2} \ge 0\\{\left( {m - a} \right)^2} \ge 0\end{array} \right.\)\( \Rightarrow 5{a^2} + {m^2} + {\left( {m - a} \right)^2} > 0,\forall m\)
Tam giác AB’C’ vuông ở B’ khi và chỉ khi :
\(\begin{array}{l}AB{'^2} + B'C{'^2} = AC{'^2}\\ \Leftrightarrow 2{a^2} + 4{a^2} + {\left( {m - a} \right)^2} = 3{a^2} + {m^2}\\ \Leftrightarrow 6{a^2} + {m^2} - 2ma + {a^2} - 3{a^2} - {m^2} = 0\\ \Leftrightarrow 4{a^2} - 2ma = 0\\ \Leftrightarrow 2ma = 4{a^2}\\ \Leftrightarrow m = 2a\end{array}\)
Vậy tam giác AB’C’ vuông ở B’ khi và chỉ khi m = 2a
b. Giả sử tam giác AB’C’ vuông ở B’, tức là m = 2a
Tam giác ABC vuông tại A có đường cao AH nên:
\(BH.BC = A{B^2}\)\( \Leftrightarrow BH = \frac{{A{B^2}}}{{BC}} = \frac{{{a^2}}}{{2a}} = \frac{a}{2}\)
\( \Rightarrow HC = BC - BH\) \( = 2a - \frac{a}{2} = \frac{{3a}}{2}\)
Tam giác B’BH vuông tại B nên:
\(B'{H^2} = B'{B^2} + B{H^2}\) \( = {a^2} + {\left( {\frac{a}{2}} \right)^2} = \frac{{5{a^2}}}{4}\)
Tam giác C’CH vuông tại C nên:
\(C'{H^2} = C'{C^2} + C{H^2}\) \( = {\left( {2a} \right)^2} + {\left( {\frac{{3a}}{2}} \right)^2} = \frac{{25{a^2}}}{4}\)
\(B'C{'^2} = 4{a^2} + {\left( {2a - a} \right)^2} = 5{a^2}\)
\( \Rightarrow B'{H^2} + B'C{'^2}\) \( = \frac{{5{a^2}}}{4} + 5{a^2} = \frac{{25{a^2}}}{4} = C'{H^2}\)
\( \Rightarrow \Delta B'C'H\) vuông tại B’.
*) Tính góc giữa mp(ABC) và mp(AB’C’) khi m = 2a.
Gọi I là giao điểm của B’C’ và BC.
Do BB’ // CC’ , BB’ = a, CC’ = 2a nên BB' là đường trung bình của tam giác ICC'
Do đó BC = BI, B’C’ = B’I.
Xét phép chiếu lên mp(ABC). Ta có tam giác AIC là hình chiếu của tam giác AIC’. Gọi φ là góc giữa mp(ABC) và mp(AB’C’) thì \({S_{AIC}} = {S_{AIC'}}\cos \varphi \)
Ta có: \({S_{AIC}} = 2{S_{ABC}} \)\( = 2.\frac{1}{2}AB.AC = 2.\frac{1}{2}.a.a\sqrt 3 = {a^2}\sqrt 3 \)
Mặt khác : \({S_{AIC'}} = {1 \over 2}IC'.AB' \)\(= {1 \over 2}.2a\sqrt 5 .a\sqrt 2 = {a^2}\sqrt {10} \)
Từ đó : \(\cos \varphi = {{{a^2}\sqrt 3 } \over {{a^2}\sqrt {10} }} = {{\sqrt {30} } \over {10}}\)
Vậy góc giữa mp(ABC) và mp(AB’C’) là φ được tính bởi \(\cos \varphi = {{\sqrt {30} } \over {10}},0^\circ < \varphi < 90^\circ \)
.
