Giải Câu 4 Trang 78 SGK Hình Học 11 Nâng Cao

Câu 4 trang 78 SGK Hình học 11 Nâng cao

Giải Câu 4 Trang 78 SGK Hình Học 11 Nâng Cao

Câu 4 trang 78 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết.

Tại tusach.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng giải toán.

Cho hai hình bình hành ABCD VÀ ABEF nằm trong hai mặt phẳng khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC, BF sao cho MC = 2AM, NF = 2BN. Qua M, N, kẻ các đường thẳng song song với AB cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:

Đề bài

a. MN // DE

b. M₁N₁ // mp(DEF)

c. mp(MNN₁M₁) // mp(DEF)

Lời giải chi tiết

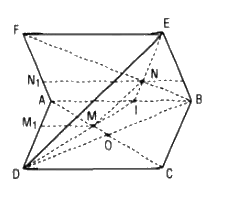
Câu 4 trang 78 SGK Hình học 11 Nâng cao 1

a. Gọi O là tâm hình bình hành ABCD, ta có AO là trung tuyến và \({{AM} \over {AO}} = {{2AM} \over {AC}} = {2 \over 3}\)

⇒ M là trọng tâm của tam giác ABD , tương tự N là trọng tâm tam giác ABE

Gọi I là trung điểm của AB thì M, N lần lượt trên DI và EI

Trong tam giác IDE ta có: \({{IM} \over {ID}} = {{IN} \over {IE}} = {1 \over 3}\) nên MN // DE và \(MN = {1 \over 3}DE\)

b. Trong ∆FAB: NN₁ // AB ⇒ \({{A{N_1}} \over {AF}} = {{BN} \over {BF}} = {1 \over 3}\)

Trong ∆DAC: MM₁ // CD ⇒ \({{A{M_1}} \over {AD}} = {{AM} \over {AC}} = {1 \over 3}\)

Do đó \({{A{N_1}} \over {AF}} = {{A{M_1}} \over {AD}}\) nên M₁N₁ // DF

Mà DF ⊂ (DEF) suy ra M₁N₁ // mp(DEF)

c. Ta có : M₁N₁ // DF , NN₁ // EF

mà M₁N₁ và NN₁ cắt nhau và nằm trong mp(MNN₁M₁), còn DF và EF cắt nhau và nằm trong mp(DEF)

Vậy mp(MNN₁M₁) // mp(DEF)

Giải Chi Tiết Câu 4 Trang 78 SGK Hình Học 11 Nâng Cao

Câu 4 trang 78 SGK Hình học 11 Nâng cao thường xoay quanh các bài toán liên quan đến việc xác định mối quan hệ giữa đường thẳng và mặt phẳng trong không gian, sử dụng các công cụ như vectơ chỉ phương, vectơ pháp tuyến, và các tính chất của hình học không gian.

Nội Dung Bài Toán Thường Gặp

Các dạng bài tập thường gặp trong câu 4 trang 78 bao gồm:

Xác định vị trí tương đối giữa đường thẳng và mặt phẳng (song song, vuông góc, cắt nhau).
Tính góc giữa đường thẳng và mặt phẳng.
Tính khoảng cách từ một điểm đến mặt phẳng.
Chứng minh các đẳng thức vectơ liên quan đến đường thẳng và mặt phẳng.

Phương Pháp Giải Toán

Để giải quyết hiệu quả các bài toán trong câu 4 trang 78, bạn cần nắm vững các kiến thức sau:

Vectơ chỉ phương của đường thẳng: Vectơ này cho biết hướng của đường thẳng.
Vectơ pháp tuyến của mặt phẳng: Vectơ này vuông góc với mọi vectơ nằm trong mặt phẳng.
Điều kiện song song, vuông góc, cắt nhau giữa đường thẳng và mặt phẳng: Sử dụng tích vô hướng và tích có hướng để kiểm tra các điều kiện này.
Công thức tính góc giữa đường thẳng và mặt phẳng: Sử dụng sin của góc bằng tỉ số giữa tích vô hướng của vectơ chỉ phương và vectơ pháp tuyến với tích của độ dài hai vectơ đó.
Công thức tính khoảng cách từ điểm đến mặt phẳng: Sử dụng công thức dựa trên phương trình mặt phẳng và tọa độ điểm.

Ví Dụ Minh Họa

Bài toán: Cho đường thẳng (d) có phương trình tham số: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P) có phương trình: 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa (d) và (P).

Giải:

Vectơ chỉ phương của (d) là a = (1, -1, 2). Vectơ pháp tuyến của (P) là n = (2, -1, 1).

Ta có a.n = 1*2 + (-1)*(-1) + 2*1 = 5 ≠ 0. Do đó, đường thẳng (d) và mặt phẳng (P) cắt nhau.

Lưu Ý Quan Trọng

Khi giải các bài toán về đường thẳng và mặt phẳng, hãy chú ý:

Kiểm tra kỹ các điều kiện trước khi áp dụng công thức.
Sử dụng đúng công thức và đơn vị.
Vẽ hình minh họa để dễ dàng hình dung bài toán.

Tài Liệu Tham Khảo

Ngoài SGK, bạn có thể tham khảo thêm các tài liệu sau:

Sách bài tập Hình học 11 Nâng cao.
Các trang web học toán trực tuyến uy tín.
Các video hướng dẫn giải toán trên YouTube.

Tổng Kết

Câu 4 trang 78 SGK Hình học 11 Nâng cao là một bài toán quan trọng, đòi hỏi sự nắm vững kiến thức và kỹ năng vận dụng linh hoạt. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, bạn sẽ tự tin hơn khi đối mặt với bài toán này. Chúc bạn học tốt!

Câu 4 trang 78 SGK Hình học 11 Nâng cao