Giải Câu 2 Trang 223 SGK Đại số và Giải tích 11 Nâng cao

Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao

Bài tập này thuộc chương trình học Đại số và Giải tích 11 Nâng cao, tập trung vào việc rèn luyện kỹ năng giải quyết các bài toán liên quan đến hàm số và đồ thị hàm số.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và phương pháp giải bài tập hiệu quả.

Giải phương trình

Đề bài

Giải phương trình

\(\tan x = \cot 2x\)

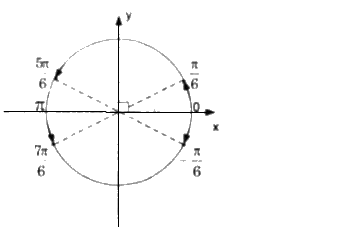
Biểu diễn các nghiệm trên đường tròn lượng giác.

Lời giải chi tiết

Điều kiện

\(\left\{ \begin{array}{l}\cos x \ne 0\\\sin 2x = 2\sin x\cos x \ne 0\end{array} \right.\)

\( \Leftrightarrow \left\{ {\matrix{ {\sin x \ne 0} \cr {\cos x \ne 0} \cr } } \right. \Leftrightarrow x \ne k{\pi \over 2}\)

\(\eqalign{ & \tan x = \cot 2x \Leftrightarrow {{\sin x} \over {\cos x}} = {{\cos 2x} \over {\sin 2x}} \cr& \Rightarrow\cos x \cos 2x - \sin x\sin 2x = 0 \cr & \Leftrightarrow \cos 3x = 0 \cr & \Leftrightarrow 4{\cos ^3}x - 3\cos x = 0\cr &\Leftrightarrow \cos x\left( {4{{\cos }^2}x - 3} \right) = 0 \cr & \Leftrightarrow {\cos ^2}x = {3 \over 4} (do\, \cos x\ne 0) \cr & \Leftrightarrow {{1 + \cos 2x} \over 2} = {3 \over 4} \Leftrightarrow \cos 2x = {1 \over 2} \cr & \Leftrightarrow x =\pm {\pi \over 6} + k\pi (k\in\mathbb Z) \cr} \)

Biểu diễn nghiệm trên đường tròn được 4 điểm.

Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao 1

Cách khác:

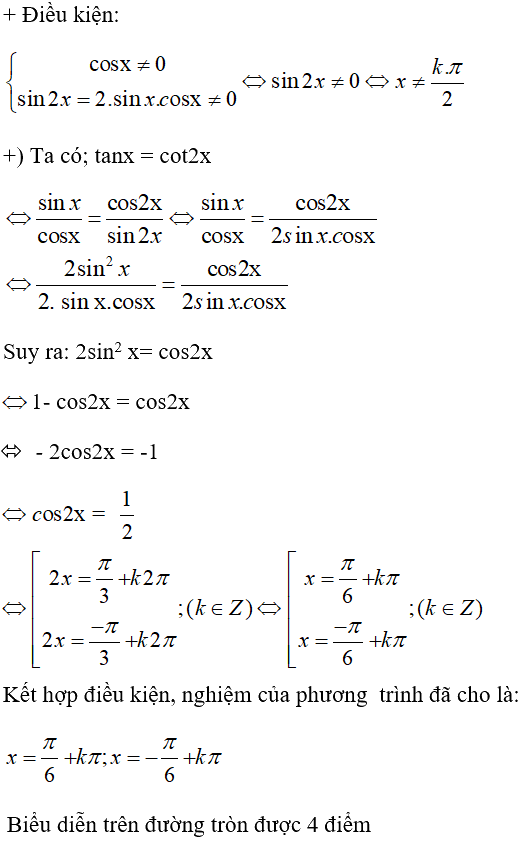
Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao 2

Giải Chi Tiết Câu 2 Trang 223 SGK Đại số và Giải tích 11 Nâng cao

Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao thường xoay quanh việc xét tính đơn điệu của hàm số, tìm cực trị, hoặc vẽ đồ thị hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, và các bước vẽ đồ thị hàm số.

Các Bước Giải Quyết Bài Toán

Xác định tập xác định của hàm số: Tìm khoảng mà hàm số có nghĩa.
Tính đạo hàm cấp nhất: Tính f'(x).
Tìm các điểm tới hạn: Giải phương trình f'(x) = 0 để tìm các điểm mà đạo hàm bằng 0 hoặc không xác định.
Xác định dấu của đạo hàm: Lập bảng xét dấu f'(x) trên các khoảng xác định bởi các điểm tới hạn.
Kết luận về tính đơn điệu:
- Nếu f'(x) > 0 trên một khoảng, hàm số đồng biến trên khoảng đó.
- Nếu f'(x) < 0 trên một khoảng, hàm số nghịch biến trên khoảng đó.
Tìm cực trị: Sử dụng điều kiện cần và đủ để hàm số đạt cực trị.
Vẽ đồ thị hàm số: Dựa vào các thông tin đã tìm được (tập xác định, đạo hàm, cực trị, giới hạn) để vẽ đồ thị hàm số.

Ví dụ Minh Họa (Giả định nội dung câu 2):

Giả sử câu 2 yêu cầu xét tính đơn điệu của hàm số: f(x) = x³ - 3x² + 2

Giải:

Tập xác định: D = ℝ
Đạo hàm: f'(x) = 3x² - 6x
Điểm tới hạn: 3x² - 6x = 0 => x = 0 hoặc x = 2
Bảng xét dấu f'(x):
x -∞ 0 2 +∞
f'(x) + - +
f(x) Đồng biến Nghịch biến Đồng biến
Kết luận: Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	Đồng biến	Nghịch biến	Đồng biến

Lưu Ý Quan Trọng

Khi giải các bài toán về hàm số, cần chú ý đến việc kiểm tra lại các bước tính toán và kết luận. Việc vẽ đồ thị hàm số cũng giúp kiểm tra tính đúng đắn của kết quả.

Tusach.vn - Nguồn Tài Liệu Học Tập Tin Cậy

Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập trong SGK Đại số và Giải tích 11 Nâng cao. Hãy truy cập website của chúng tôi để tìm hiểu thêm và nâng cao kiến thức của bạn!

Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao

Câu 2 trang 223 SGK Đại số và Giải tích 11 Nâng cao

Giải Chi Tiết Câu 2 Trang 223 SGK Đại số và Giải tích 11 Nâng cao

Các Bước Giải Quyết Bài Toán

Ví dụ Minh Họa (Giả định nội dung câu 2):

Lưu Ý Quan Trọng

Tusach.vn - Nguồn Tài Liệu Học Tập Tin Cậy

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN