Câu 2 trang 124 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Câu 2 Trang 124 SGK Hình học 11 Nâng cao
Bài tập Câu 2 trang 124 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian.
Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, đặc biệt là các phép toán vectơ để giải quyết các bài toán liên quan đến hình học không gian.
Dưới đây là lời giải chi tiết và cách làm bài tập Câu 2 trang 124 SGK Hình học 11 Nâng cao, giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng cần thiết.
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
Đề bài
Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD và DA. Kẻ MM’, NN’, PP’, QQ’ lần lượt vuông góc với CD, DA, AB, BC.
a. Gọi I là giao điểm của MP và NQ. Phép đối xứng tâm ĐI biến các đường thẳng MM’, NN’, PP’, QQ’ thành những đường thẳng nào ?
b. Chứng tỏ rằng bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại một điểm. Nhận xét gì về vị trí điểm đồng quy và hai điểm I, O?
Lời giải chi tiết
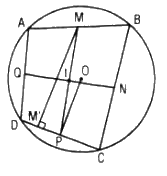
a. MNPQ là hình bình hành nên I là trung điểm
của MP và NQ.
Phép đối xứng tâm ĐI biến điểm M thành điểm P, biến đường thẳng MM’ thành đường thẳng đi qua P và song song với MM’, tức là vuông góc với DC.
Vậy đường thẳng MM’ được biến thành đường thẳng PO. Hoàn toàn tương tự : đường thẳng NN’ biến thành đường QO, đường thẳng PP’ biến thành đường MO, đường thẳng QQ’ biến thành đường NO.
b. Vì bốn đường thẳng MO, NO, PO, QO đồng quy tại điểm O nên bốn đường thẳng MM’, NN’, PP’, QQ’ đồng quy tại O’ đối xứng với O qua điểm I.
Giải Chi Tiết Câu 2 Trang 124 SGK Hình Học 11 Nâng Cao
Câu 2 trang 124 SGK Hình học 11 Nâng cao thường xoay quanh việc áp dụng các kiến thức về vectơ trong không gian để chứng minh các tính chất hình học hoặc giải quyết các bài toán liên quan đến vị trí tương đối của các điểm, đường thẳng và mặt phẳng.
Phân Tích Đề Bài và Xác Định Yêu Cầu
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Xác định các điểm, vectơ, và mối quan hệ giữa chúng được đề cập trong bài. Việc vẽ hình minh họa cũng rất hữu ích để hình dung rõ hơn về bài toán.
Các Kiến Thức Liên Quan Cần Nắm Vững
- Vectơ trong không gian: Định nghĩa, các phép toán cộng, trừ, nhân với một số thực, tích vô hướng, tích có hướng.
- Các tính chất của tích vô hướng và tích có hướng: Sử dụng để chứng minh vuông góc, song song, đồng phẳng.
- Hệ tọa độ trong không gian: Biểu diễn vectơ, điểm trong hệ tọa độ.
- Ứng dụng của vectơ trong hình học không gian: Chứng minh các tính chất hình học, tính khoảng cách, góc.
Lời Giải Chi Tiết (Ví dụ minh họa - đề bài cụ thể cần được thay thế)
Giả sử đề bài: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
- Chọn hệ tọa độ: Đặt A(0;0;0), B(a;0;0), C(a;a;0), D(0;a;0), S(0;0;a).
- Tìm vectơ:\overrightarrow{SC} = (a; a; -a)
- Tìm vectơ pháp tuyến của mặt phẳng (ABCD):\overrightarrow{n} = (0; 0; 1)
- Tính góc: Góc \alpha giữa SC và mặt phẳng (ABCD) được tính bởi công thức: sin(\alpha) = \frac{|\overrightarrow{SC} \cdot \overrightarrow{n}|}{|\overrightarrow{SC}| |\overrightarrow{n}|}
- Thay số và tính toán:sin(\alpha) = \frac{|-a|}{\sqrt{a^2 + a^2 + a^2} \cdot 1} = \frac{a}{\sqrt{3}a} = \frac{1}{\sqrt{3}}
- Kết luận:\alpha = arcsin(\frac{1}{\sqrt{3}})
Các Dạng Bài Tập Thường Gặp và Phương Pháp Giải
Ngoài dạng bài tập tính góc như ví dụ trên, Câu 2 trang 124 SGK Hình học 11 Nâng cao còn có thể gặp các dạng bài tập sau:
- Chứng minh các điểm cùng thuộc một mặt phẳng: Sử dụng tích có hướng để chứng minh ba vectơ đồng phẳng.
- Chứng minh các đường thẳng song song, vuông góc: Sử dụng tích vô hướng để chứng minh.
- Tính khoảng cách giữa hai điểm, giữa điểm và mặt phẳng: Sử dụng công thức tính khoảng cách.
Lưu Ý Khi Giải Bài Tập
Để giải bài tập Hình học 11 Nâng cao một cách hiệu quả, cần lưu ý những điều sau:
- Vẽ hình minh họa: Giúp hình dung rõ hơn về bài toán.
- Chọn hệ tọa độ phù hợp: Giúp đơn giản hóa bài toán.
- Sử dụng các công thức một cách chính xác: Tránh sai sót trong tính toán.
- Kiểm tra lại kết quả: Đảm bảo tính chính xác của đáp án.
Tài Liệu Tham Khảo Hữu Ích
Để nâng cao kiến thức và kỹ năng giải bài tập Hình học 11 Nâng cao, các em có thể tham khảo các tài liệu sau:
- Sách giáo khoa Hình học 11 Nâng cao
- Sách bài tập Hình học 11 Nâng cao
- Các trang web học toán trực tuyến uy tín như tusach.vn
Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải Câu 2 trang 124 SGK Hình học 11 Nâng cao và các bài tập tương tự. Chúc các em học tốt!