Câu 38 trang 68 SGK Hình học 11 Nâng cao
Tổng quan nội dung
Giải Bài Tập Hình Học 11 Nâng Cao - Câu 38 Trang 68
Câu 38 trang 68 SGK Hình học 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng trong không gian để giải quyết các vấn đề thực tế.
Tại tusach.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu và chính xác nhất cho câu hỏi này, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
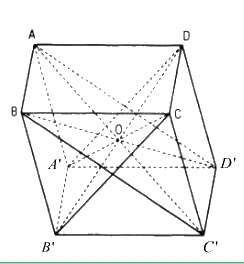
Chứng minh rẳng tổng bình phương tất cả các đường chéo của một hình hộp bằng tổng bình phương tất cả các cạnh của hình hộp đó
Đề bài
Chứng minh rẳng tổng bình phương tất cả các đường chéo của một hình hộp bằng tổng bình phương tất cả các cạnh của hình hộp đó
Phương pháp giải - Xem chi tiết
Áp dụng tính chất: “ Trong một hình bình hành, tổng bình phương hai đường chéo bằng tổng bình phương bốn cạnh.”
Chứng minh:
Ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC\cos B\\B{D^2} = A{B^2} + A{D^2} - 2AB.AD\cos A\\\,\,\,\,\,\,\,\,\,\,\, = A{B^2} + B{C^2} + 2AB.BC\cos B\end{array}\)
Vì \(AD = BC\) và \(\cos A = - \cos B\) (hai góc bù nhau thì cos đối nhau)
\( \Rightarrow A{C^2} + B{D^2} = 2A{B^2} + 2B{C^2}\) \( = 2\left( {A{B^2} + B{C^2}} \right)\).
Lời giải chi tiết
Đặt AB = a, BC = b, AA’ = c ( đó là 3 kích thước của hình hộp).
Trong hình bình hành ABC’D’ ta có:
\(AC'{^2} + BD{'^2} = 2\left( {{a^2} + BC'{^2}} \right)\) (1)
Trong hình bình hành A’B’CD ta có:
\(A'{C^2} + B'{D^2} = 2\left( {{a^2} + B'{C^2}} \right)\) (2)
Cộng (1) và (2) ta được :
\(AC'{^2} + BD'{^2}+A'{C^2} + B'{D^2} \)\(= 2\left( {2{a^2} + BC{'^2} + B'{C^2}} \right)\) (3)
Mặt khác trong hình bình hành BB’C’C ta có:
\(BC{'^2} + B'{C^2} = 2\left( {{b^2} + {c^2}} \right)\) (4)
Thay (4) vào (3) ta được :
\(AC'{^2} + BD'{^2} + A'{C^2} + B\,'{D^2}\)\( = 4\left( {{a^2} + {b^2} + {c^2}} \right)\) (đpcm).
Giải Chi Tiết Câu 38 Trang 68 SGK Hình Học 11 Nâng Cao
Câu 38 trang 68 SGK Hình học 11 Nâng cao thường xoay quanh việc xác định mối quan hệ giữa các đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, tích vô hướng, tích có hướng, phương trình đường thẳng và phương trình mặt phẳng.
Tóm Tắt Lý Thuyết Quan Trọng
- Vectơ: Định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số), tích vô hướng, tích có hướng.
- Đường Thẳng trong Không Gian: Phương trình tham số, phương trình chính tắc, vị trí tương đối giữa hai đường thẳng.
- Mặt Phẳng trong Không Gian: Phương trình mặt phẳng, vị trí tương đối giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng.
Phân Tích Bài Toán Câu 38 Trang 68
Để giải quyết câu 38 trang 68, bạn cần đọc kỹ đề bài, xác định các yếu tố quan trọng như các điểm, vectơ, đường thẳng, mặt phẳng được đề cập. Sau đó, áp dụng các công thức và định lý đã học để tìm ra mối quan hệ giữa chúng.
Ví Dụ Minh Họa (Giả định một dạng bài tập phổ biến)
Đề bài (Ví dụ): Cho điểm A(1; 2; 3) và đường thẳng d: x = t, y = t + 1, z = 2t - 1. Tìm tọa độ điểm A' đối xứng với A qua đường thẳng d.
- Tìm hình chiếu vuông góc H của A lên d: Gọi H(t; t+1; 2t-1) là hình chiếu của A lên d. Khi đó, vectơ AH vuông góc với vectơ chỉ phương của d.
- Tính vectơ AH: AH = (t-1; t+1-2; 2t-1-3) = (t-1; t-1; 2t-4)
- Vectơ chỉ phương của d: u = (1; 1; 2)
- Sử dụng tích vô hướng: AH.u = 0 => (t-1) + (t-1) + 2(2t-4) = 0 => 6t - 8 = 0 => t = 4/3
- Tìm tọa độ H: H(4/3; 7/3; 5/3)
- Tìm tọa độ A': A' là điểm đối xứng của A qua H, nên H là trung điểm của AA'. Sử dụng công thức trung điểm: xA' = 2xH - xA, yA' = 2yH - yA, zA' = 2zH - zA.
- Tính tọa độ A': A'(5/3; 11/3; 13/3)
Lưu Ý Khi Giải Bài Tập
Khi giải các bài tập về hình học không gian, bạn cần chú ý:
- Vẽ hình minh họa để dễ hình dung bài toán.
- Sử dụng các công thức và định lý một cách chính xác.
- Kiểm tra lại kết quả để đảm bảo tính đúng đắn.
Tusach.vn - Nguồn Tài Liệu Học Tập Tin Cậy
Tusach.vn là website cung cấp giải pháp học tập toàn diện cho học sinh, sinh viên. Chúng tôi cung cấp lời giải chi tiết, bài giảng video, bài tập trắc nghiệm và nhiều tài liệu học tập hữu ích khác. Hãy truy cập tusach.vn để học tốt môn Toán và các môn học khác!
| Khái niệm | Công thức |
|---|---|
| Tích vô hướng | a.b = |a||b|cos(θ) |
| Tích có hướng | [a, b] = |a||b|sin(θ)n |
| Nguồn: Sách giáo khoa Hình học 11 Nâng cao | |