Giải Câu 11 Trang 96 SGK Hình Học 11 Nâng Cao

Câu 11 trang 96 SGK Hình học 11 Nâng cao

Giải Câu 11 Trang 96 SGK Hình Học 11 Nâng Cao

Câu 11 trang 96 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài toán này thường yêu cầu học sinh vận dụng kiến thức về vectơ, đường thẳng và mặt phẳng để giải quyết.

tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và kỹ năng giải bài tập.

Cho hình tứ diện ABCD có AB = AC = AD và

LG a

AB ⊥ CD;

Lời giải chi tiết:

Ta có:

\(\eqalign{ & \overrightarrow {AB} .\overrightarrow {CD} \cr &= \overrightarrow {AB} .\left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) \cr &= \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \cr & = AB.AD.\cos \widehat {BAD} - AB.AC.\cos \widehat {BAC} = 0 \cr & \Rightarrow AB \bot CD. \cr} \)

(Vì AD=AC và \(\widehat {BAD}=\widehat {BAC}=60^0\).

LG b

Nếu I và J lần lượt là trung điểm của AB và CD thì \(IJ \bot AB\) và \(IJ \bot CD.\)

Lời giải chi tiết:

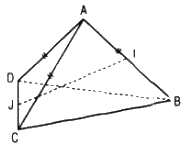
Câu 11 trang 96 SGK Hình học 11 Nâng cao 1

Ta có:

\(\eqalign{ & \overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AJ} \cr & = {1 \over 2}\overrightarrow {BA} + {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {AC} } \right) \cr & = {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {BC} } \right) \cr & = {1 \over 2}\left( {\overrightarrow {AD} + \overrightarrow {AC} - \overrightarrow {AB} } \right) \cr} \)

Suy ra :

\(\eqalign{ & \overrightarrow {AB} .\overrightarrow {IJ} = {1 \over 2}\left( {\overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} - A{B^2}} \right) \cr & ={1 \over 2} \left( {AB.AD.\cos 60^\circ } + AB.AC.\cos 60^\circ - A{B^2} \right) \cr&= 0 \cr & \Rightarrow AB \bot IJ \cr} \)

Mặt khác :

\(\eqalign{ & \overrightarrow {CD} .\overrightarrow {IJ} = {1 \over 2}\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right).\left( {\overrightarrow {AD} + \overrightarrow {BA} + \overrightarrow {AC} } \right) \cr & = {1 \over 2}\left( { - \overrightarrow {AC} .\overrightarrow {AD} + {{\overrightarrow {AD} }^2} + \overrightarrow {CA} .\overrightarrow {BA} + \overrightarrow {AD} .\overrightarrow {BA} - {{\overrightarrow {AC} }^2} + \overrightarrow {AD} .\overrightarrow {AC} } \right) \cr & = - {1 \over 2}\overrightarrow {AB} .\left( {\overrightarrow {CA} + \overrightarrow {AD} } \right) = - {1 \over 2}\overrightarrow {AB} .\overrightarrow {CD} = 0 \cr & \Rightarrow CD \bot IJ \cr} \)

Giải Chi Tiết Câu 11 Trang 96 SGK Hình Học 11 Nâng Cao

Câu 11 trang 96 SGK Hình học 11 Nâng cao thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, các phép toán vectơ, điều kiện đồng phẳng của ba vectơ, và phương trình mặt phẳng.

Đề Bài Câu 11 Trang 96 SGK Hình Học 11 Nâng Cao

(Đề bài cụ thể của câu 11 sẽ được chèn vào đây. Ví dụ: Cho bốn điểm A, B, C, D không đồng phẳng. Chứng minh rằng bốn điểm đó tạo thành một tứ diện.)

Lời Giải Chi Tiết

Để chứng minh bốn điểm A, B, C, D tạo thành một tứ diện, ta cần chứng minh rằng bốn điểm này không đồng phẳng. Điều này có nghĩa là ba vectơ AB, AC, và AD không đồng phẳng.

Để chứng minh ba vectơ không đồng phẳng, ta có thể tính tích hỗn hợp của chúng. Nếu tích hỗn hợp khác 0, thì ba vectơ đó không đồng phẳng.

Tích hỗn hợp của ba vectơ AB, AC, và AD được tính như sau:

[AB, AC, AD] = (AB x AC) . AD

Trong đó:

AB x AC là tích vector của AB và AC.
(AB x AC) . AD là tích vô hướng của tích vector (AB x AC) và AD.

Nếu kết quả của tích hỗn hợp khác 0, thì bốn điểm A, B, C, D không đồng phẳng và do đó tạo thành một tứ diện.

Ví Dụ Minh Họa

Giả sử A(1; 2; 3), B(2; 3; 4), C(3; 4; 5), D(4; 5; 6). Ta tính:

AB = (1; 1; 1)

AC = (2; 2; 2)

AD = (3; 3; 3)

Ta thấy AC = 2AB và AD = 3AB. Điều này có nghĩa là ba vectơ AB, AC, và AD cùng phương, do đó chúng đồng phẳng. Vậy bốn điểm A, B, C, D đồng phẳng và không tạo thành một tứ diện.

Lưu Ý Quan Trọng

Khi giải các bài toán về đường thẳng và mặt phẳng trong không gian, học sinh cần chú ý:

Nắm vững các định nghĩa và tính chất cơ bản.
Sử dụng thành thạo các phép toán vectơ.
Kiểm tra kỹ các điều kiện để đảm bảo tính chính xác của kết quả.

Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự trong SGK và sách bài tập Hình học 11 Nâng cao.

Hy vọng lời giải chi tiết này sẽ giúp các em hiểu rõ hơn về Câu 11 trang 96 SGK Hình học 11 Nâng cao. Chúc các em học tốt!

Câu 11 trang 96 SGK Hình học 11 Nâng cao