Giải Câu 19 Trang 103 SGK Hình Học 11 Nâng Cao

Câu 19 trang 103 SGK Hình học 11 Nâng cao

Giải Câu 19 Trang 103 SGK Hình Học 11 Nâng Cao

Câu 19 trang 103 SGK Hình học 11 Nâng cao là một bài toán quan trọng trong chương trình học Hình học không gian. Bài toán này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng để giải quyết.

Dưới đây là lời giải chi tiết, dễ hiểu, cùng với phương pháp giải và đáp án chính xác, được cung cấp bởi đội ngũ giáo viên chuyên môn của tusach.vn.

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC.

Đề bài

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm tam giác ABC.

a. Chứng minh rằng SG ⊥ (ABC). Tính SG.

b. Xét mặt phẳng (P) đi qua A và vuông góc với đường thẳng SC. Tìm hệ thức liên hệ giữa a và b để (P) cắt SC tại điểm C₁ nằm giữa S và C. Khi đó hãy tính diện tích thiết diện của hình chóp S.ABC khi cắt bởi mp(P).

Lời giải chi tiết

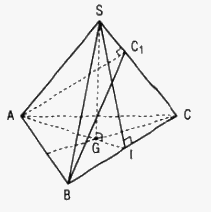
Câu 19 trang 103 SGK Hình học 11 Nâng cao 1

a. Gọi I là trung điểm của BC.

Tam giác ABC đều, AI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ AI.

Tam giác SBC có SB = SC, SI là đường trung tuyến nên đồng thời là đường cao: BC ⊥ SI.

\(\begin{array}{l} \Rightarrow BC \bot (SAI) \supset SG\\ \Rightarrow BC \bot SG.\,\,\, (1)\end{array}\)

Chứng minh tương tự ta có: \(AB \bot SG\,\,\, (1)\)

Từ (1;2) suy ra \(SG \bot (ABC)\)

\(\begin{array}{l}+) \, SI^2 ={S{C^2} - I{C^2}} ={{b^2} - \frac{{{a^2}}}{4}} \\+) \, GI = \frac{1}{3}AI;\, AI ^2 = {A{B^2} - B{I^2}} =a.\frac{{3 }}{4} \Rightarrow GI= \frac{{a\sqrt 3 }}{6}.\end{array}\)

\(\Rightarrow SG = \sqrt {S{I^2} - G{I^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{4} - {{{a^2}} \over {12}}} \) \( = \sqrt {{{12{b^2} - 4{a^2}} \over {12}}}\) \( = \sqrt {{{3{b^2} - {a^2}} \over 3}} \)

b. Kẻ AC₁ ⊥ SC thì (P) chính là mp(ABC₁)

Vì SAC là tam giác cân mà AC₁ ⊥ SC nên C₁ nằm giữa S và C khi và chỉ khi

\(\widehat {ASC} < 90^\circ \Leftrightarrow A{S^2} + C{S^2} > A{C^2} \) \(\Leftrightarrow 2{b^2} > {a^2}\)

Ta có : AB ⊥ GC và AB ⊥ SG ⇒ AB ⊥ SC

SC ⊥ AC₁ và SC ⊥ AB nên SC ⊥ (ABC₁)

Thể tích tứ diện SABC là :

\(\eqalign{ & {V_{SABC}} = {1 \over 3}SG.{S_{ABC}} = {1 \over 3}SC.{S_{AB{C_1}}} \cr & \Rightarrow {S_{AB{C_1}}} = {{SG.{S_{ABC}}} \over {SC}} \cr &= {{\sqrt {{{3{b^2} - {a^2}} \over 3}} .{{{a^2}\sqrt 3 } \over 4}} \over b} = {{{a^2}\sqrt {3{b^2} - {a^2}} } \over {4b}} \cr} \)

Giải Chi Tiết Câu 19 Trang 103 SGK Hình Học 11 Nâng Cao

Câu 19 trang 103 SGK Hình học 11 Nâng cao thuộc chương trình Hình học không gian, cụ thể là phần kiến thức về đường thẳng và mặt phẳng trong không gian. Bài toán này thường yêu cầu học sinh chứng minh một đường thẳng song song với một mặt phẳng, hoặc xác định giao điểm của đường thẳng và mặt phẳng.

Nội dung Bài Toán

Để hiểu rõ hơn về bài toán, chúng ta cần xem lại nội dung chính của câu 19 trang 103. (Giả sử nội dung bài toán là: Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Gọi M là trung điểm của CD. Chứng minh rằng AM song song với mặt phẳng (SBC).)

Phương Pháp Giải

Để chứng minh một đường thẳng song song với một mặt phẳng, ta có thể sử dụng một trong các phương pháp sau:

Phương pháp 1: Sử dụng định nghĩa đường thẳng song song với mặt phẳng. Chứng minh đường thẳng không nằm trong mặt phẳng và không có điểm chung với mặt phẳng.
Phương pháp 2: Sử dụng định lý về đường thẳng song song với mặt phẳng. Chứng minh đường thẳng song song với một đường thẳng nằm trong mặt phẳng, và đường thẳng đó không nằm trong mặt phẳng.
Phương pháp 3: Sử dụng tính chất của hình chóp và hình hộp. Áp dụng các tính chất đặc trưng của các hình này để chứng minh.

Lời Giải Chi Tiết

Trong bài toán này, ta sẽ sử dụng phương pháp 2. Cụ thể:

Bước 1: Xác định các yếu tố liên quan. Ta có M là trung điểm của CD, và ABCD là hình vuông. Do đó, AM là đường trung bình của hình vuông ABCD.
Bước 2: Chứng minh AM song song với BC. Vì ABCD là hình vuông, nên BC song song với AD. Mà AM là đường trung bình của hình vuông ABCD, nên AM song song với BC.
Bước 3: Chứng minh AM song song với mặt phẳng (SBC). Vì AM song song với BC và BC nằm trong mặt phẳng (SBC), nên AM song song với mặt phẳng (SBC).

Lưu Ý Quan Trọng

Khi giải các bài toán về đường thẳng và mặt phẳng, cần chú ý:

Vẽ hình chính xác và rõ ràng.
Nắm vững các định nghĩa, định lý và tính chất liên quan.
Phân tích bài toán một cách logic và tìm ra phương pháp giải phù hợp.

Bài Tập Tương Tự

Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:

Bài 20 trang 103 SGK Hình học 11 Nâng cao
Bài 21 trang 105 SGK Hình học 11 Nâng cao

Kết Luận

Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên, các em học sinh đã hiểu rõ cách giải Câu 19 trang 103 SGK Hình học 11 Nâng cao. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt trong các kỳ thi.

Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ nhé!

Câu 19 trang 103 SGK Hình học 11 Nâng cao