Giải Câu 55 Trang 221 SGK Đại số và Giải tích 11 Nâng cao

Câu 55 trang 221 SGK Đại số và Giải tích 11 Nâng cao

Giải Bài Tập Đại Số và Giải Tích 11 Nâng Cao - Câu 55 Trang 221

Câu 55 trang 221 SGK Đại số và Giải tích 11 Nâng cao là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số, đạo hàm để giải quyết các vấn đề thực tế.

Tại tusach.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.

Đồ thị (P) của một hàm số bậc hai

Đề bài

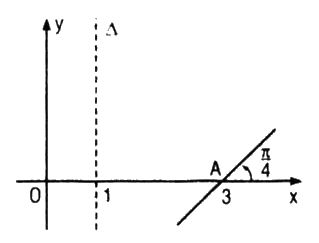
Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng ∆, điểm A thuộc (P) và tiếp tuyến tại A của (P) (h. 5.8). Hãy tìm P(x) và vẽ lại đồ thị (P).

Câu 55 trang 221 SGK Đại số và Giải tích 11 Nâng cao 1

Lời giải chi tiết

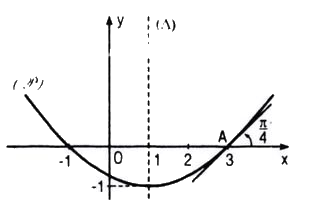
Câu 55 trang 221 SGK Đại số và Giải tích 11 Nâng cao 2

Đa thức phải tìm có dạng : \(P\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\)

Ta có: \(P'\left( x \right) = 2ax + b\)

Vì trục đối xứng (∆) có phương trình x = 1 nên : \( - {b \over {2a}} = 1\,\,\left( 1 \right)\)

Vì đồ thị (P) đi qua điểm A(3 ; 0) nên ta có P(3) = 0, tức là:

\(9a + 3b + c = 0\,\,\left( 2 \right)\)

Vì hệ số góc của tiếp tuyến tại điểm A(3 ; 0) bằng \(\tan {\pi \over 4}\) nên ta có \(P’(3) = 1\), tức là :

\(6a + b = 1\,\left( 3 \right)\)

Giải hệ ba phương trình (1), (2) và (3) với ba ẩn số a, b và c, ta được :

\(\eqalign{ & a = {1 \over 4} \cr & b = - {1 \over 2} \cr & c = - {3 \over 4} \cr} \)

Vậy \(P\left( x \right) = {1 \over 4}{x^2} - {1 \over 2}x - {3 \over 4}\)

Giải Chi Tiết Câu 55 Trang 221 SGK Đại Số và Giải Tích 11 Nâng Cao

Câu 55 trang 221 SGK Đại số và Giải tích 11 Nâng cao thường liên quan đến việc xét tính đơn điệu của hàm số. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức sau:

Đạo hàm của hàm số: Tính đạo hàm f'(x) của hàm số đã cho.
Xét dấu đạo hàm: Xác định khoảng mà f'(x) > 0 (hàm số đồng biến) và khoảng mà f'(x) < 0 (hàm số nghịch biến).
Kết luận về tính đơn điệu: Dựa vào dấu của đạo hàm để kết luận về tính đơn điệu của hàm số trên các khoảng xác định.

Ví dụ minh họa (giả định nội dung câu 55):

Giả sử câu 55 yêu cầu xét tính đơn điệu của hàm số f(x) = x³ - 3x² + 2.

Tính đạo hàm: f'(x) = 3x² - 6x
Giải phương trình f'(x) = 0: 3x² - 6x = 0 => x(x - 2) = 0 => x = 0 hoặc x = 2
Xét dấu đạo hàm:
x -∞ 0 2 +∞
f'(x) + - +
f(x) Đồng biến Nghịch biến Đồng biến
Kết luận: Hàm số f(x) đồng biến trên các khoảng (-∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2).

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	Đồng biến	Nghịch biến	Đồng biến

Mẹo giải nhanh và hiệu quả

Để giải nhanh các bài tập về tính đơn điệu, bạn nên:

Nắm vững các công thức đạo hàm cơ bản.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng bảng xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến một cách chính xác.

Lưu ý quan trọng

Khi giải bài tập về tính đơn điệu, cần chú ý đến tập xác định của hàm số. Hàm số chỉ được xét tính đơn điệu trên tập xác định của nó.

Tusach.vn - Đồng hành cùng bạn học tập

Tusach.vn luôn cập nhật lời giải chi tiết, chính xác cho tất cả các bài tập trong SGK Đại số và Giải tích 11 Nâng cao. Hãy truy cập tusach.vn để học tập hiệu quả và đạt kết quả cao trong môn Toán!

Các bài tập tương tự

Bạn có thể tham khảo thêm các bài tập tương tự về tính đơn điệu của hàm số trong SGK và sách bài tập Đại số và Giải tích 11 Nâng cao.